题目内容
【题目】记实数x1 , x2 , …,xn中最小数为min{x1 , x2 , …,xn},则定义在区间[0,+∞)上的函数f(x)=min{x2+1,x+3,13﹣x}的最大值为( )
A.5
B.6
C.8
D.10
【答案】C
【解析】解:在同一坐标系中作出三个函数y=x2+1,y=x+3,
y=13﹣x的图象如图:
由图可知,min{x2+1,x+3,13﹣x}为y=x+3上A点下方的射线,
抛物线AB之间的部分,线段BC,与直线y=13﹣x点C下方的部分的组合体,
显然,在C点时,y=min{x2+1,x+3,13﹣x}取得最大值.
解方程组 ![]() 得,C(5,8),
得,C(5,8),
∴max{min{x2+1,x+3,13﹣x}}=8.
故选:C.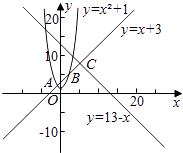
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.

练习册系列答案
相关题目
