题目内容
已知函数
(1)写出函数 的单调区间;
的单调区间;
(2)若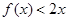 在
在 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若函数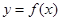 在
在 上值域是
上值域是 ,求实数
,求实数 的取值范围.
的取值范围.
(1)增区间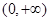 , 减区间
, 减区间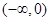 ;(2)实数
;(2)实数 的取值范围为
的取值范围为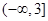
(3)实数 的取值范围为
的取值范围为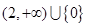
解析试题分析:(1)由已知函数可化为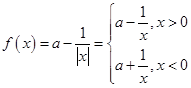 ,根据函数
,根据函数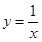 的单调区间,得出所求函数的单调区间;(2)由(1)可知不等式
的单调区间,得出所求函数的单调区间;(2)由(1)可知不等式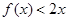 可化为
可化为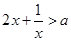 ,根据函数
,根据函数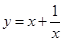 在
在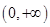 的单调性,可求得函数
的单调性,可求得函数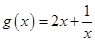 在
在 上的值域,从而求出所实数
上的值域,从而求出所实数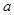 的范围;(3)由(1)可知函数
的范围;(3)由(1)可知函数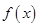 的单调区间,可将区间
的单调区间,可将区间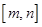 分
分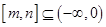 与
与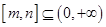 两种情况进行讨论,根据函数
两种情况进行讨论,根据函数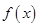 的单调性及值域,分别建立关于
的单调性及值域,分别建立关于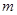 ,
,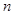 的方程组,由方程组解的情况,从而求出实数
的方程组,由方程组解的情况,从而求出实数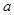 的取值范围.
的取值范围.
试题解析:(1)增区间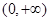 , 减区间
, 减区间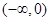 2分
2分
(2)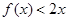 在
在 上恒成立即
上恒成立即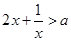 在
在 上恒成立
上恒成立
易证,函数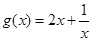 在
在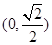 上递减,在
上递减,在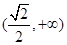 上递增
上递增
故当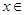
 上有
上有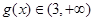
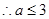
故 的取值范围为
的取值范围为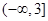 5分
5分
(3)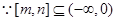 或
或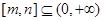
①当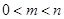 时,
时,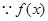 在
在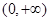 上递增,
上递增,
即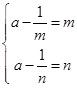 即方程
即方程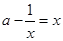 有两个不等正实数根
有两个不等正实数根
方程化为: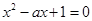 故
故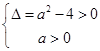 得
得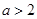 10分
10分
②当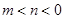 时
时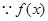 在
在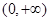 上递减
上递减 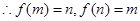
即 (1)-(2)得
(1)-(2)得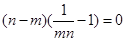
又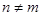 ,
,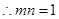
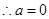 13分
13分
综合①②得实数 的取值范围为
的取值范围为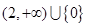 14分
14分
考点:1.分段函数;2.函数的单调性;3.分类讨论思想.

练习册系列答案
相关题目
 ,
,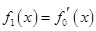 ,
,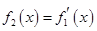 ,
,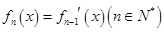 .
.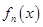 表达式(不需证明);
表达式(不需证明);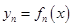 ;
;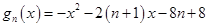 ,
, 的最大值为
的最大值为 ,
,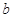 ,试求
,试求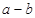 的最小值.
的最小值.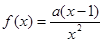 ,其中
,其中 .
. 的单调区间;
的单调区间;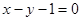 是曲线
是曲线 的切线,求实数
的切线,求实数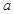 的值;
的值;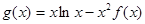 ,求
,求 在区间
在区间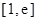 上的最小值.(
上的最小值.( 为自然对数的底数)
为自然对数的底数)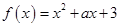 .
. 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
,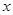 的取值范围.
的取值范围.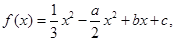 其中
其中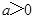 ,曲线
,曲线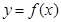 在点
在点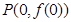 处的切线方程为
处的切线方程为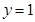 .
.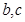 的值;
的值;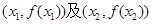 处的切线都过点(0,2).证明:当
处的切线都过点(0,2).证明:当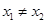 时,
时,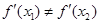 ;
; 的取值范围.
的取值范围.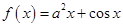 ,
,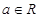 .
. 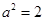 时,求
时,求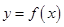 在
在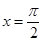 处的切线方程;
处的切线方程; 在
在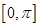 内单调递增,求
内单调递增,求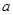 的取值范围.
的取值范围.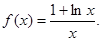
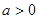 且函数
且函数 在区间
在区间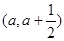 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围;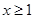 时,不等式
时,不等式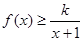 恒成立,求实数
恒成立,求实数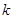 的取值范围.
的取值范围.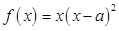 ,
,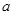 是大于零的常数.
是大于零的常数.  时,求
时,求 的极值;
的极值; 上为单调递增,求实数
上为单调递增,求实数 上存在一点
上存在一点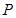 ,使得曲线
,使得曲线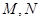 ,且
,且 成立.
成立.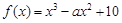 ,
,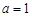 时,求曲线
时,求曲线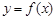 在点
在点 处的切线方程;
处的切线方程;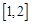 内至少存在一个实数
内至少存在一个实数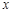 ,使得
,使得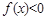 成立,求实数
成立,求实数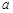 的取值范围.
的取值范围.