题目内容
已知直线l1:x-2y-1=0,直线l2:ax-by+1=0,其中a,b∈{1,2,3,4,5,6}.
(1) 求直线l1与l2相交的概率;
(2) 求直线l1与l2的交点位于第一象限的概率.
(1) 求直线l1与l2相交的概率;
(2) 求直线l1与l2的交点位于第一象限的概率.
(1)  (2)
(2) 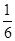
 (2)
(2) 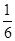
(1) 直线l1的斜率k1= ,直线l2的斜率k2=
,直线l2的斜率k2=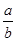 .设事件A为“直线l1与l2相交”.a,b∈{1,2,3,4,5,6}的总事件数为(1,1),(1,2),…,(1,6),(2,1),(2,2),…,(2,6),…,(5,6),(6,6)共36种.若l1与l2相交,则l1∥l2,即k1=k2,即b=2a.满足条件的实数对(a,b)有(1,2),(2,4),(3,6)共三种情况.所以P(A)=
.设事件A为“直线l1与l2相交”.a,b∈{1,2,3,4,5,6}的总事件数为(1,1),(1,2),…,(1,6),(2,1),(2,2),…,(2,6),…,(5,6),(6,6)共36种.若l1与l2相交,则l1∥l2,即k1=k2,即b=2a.满足条件的实数对(a,b)有(1,2),(2,4),(3,6)共三种情况.所以P(A)= .
.
(2) 设事件B为“直线l1与l2的交点位于第一象限”,由于直线l1与l2有交点,则b≠2a.联立方程组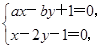 解得
解得 ∵l1与l2的交点位于第一象限,∴
∵l1与l2的交点位于第一象限,∴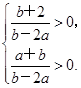
∵ a、b∈{1,2,3,4,5,6},∴ b>2a.∴ 总事件数共36种,满足b>2a的事件有(1,3),(1,4),(1,5),(1,6),(2,5),(2,6),共6种,∴ P(B)=
 ,直线l2的斜率k2=
,直线l2的斜率k2=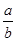 .设事件A为“直线l1与l2相交”.a,b∈{1,2,3,4,5,6}的总事件数为(1,1),(1,2),…,(1,6),(2,1),(2,2),…,(2,6),…,(5,6),(6,6)共36种.若l1与l2相交,则l1∥l2,即k1=k2,即b=2a.满足条件的实数对(a,b)有(1,2),(2,4),(3,6)共三种情况.所以P(A)=
.设事件A为“直线l1与l2相交”.a,b∈{1,2,3,4,5,6}的总事件数为(1,1),(1,2),…,(1,6),(2,1),(2,2),…,(2,6),…,(5,6),(6,6)共36种.若l1与l2相交,则l1∥l2,即k1=k2,即b=2a.满足条件的实数对(a,b)有(1,2),(2,4),(3,6)共三种情况.所以P(A)= .
.(2) 设事件B为“直线l1与l2的交点位于第一象限”,由于直线l1与l2有交点,则b≠2a.联立方程组
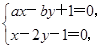 解得
解得 ∵l1与l2的交点位于第一象限,∴
∵l1与l2的交点位于第一象限,∴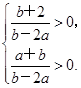
∵ a、b∈{1,2,3,4,5,6},∴ b>2a.∴ 总事件数共36种,满足b>2a的事件有(1,3),(1,4),(1,5),(1,6),(2,5),(2,6),共6种,∴ P(B)=


练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目



 条道路中抽取
条道路中抽取 条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过
条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过 的概率.
的概率. 条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:



 ppm.
ppm. 条,求
条,求 条汞含量超标的概率;
条汞含量超标的概率; 表示抽到的汞含量超标的鱼的条数.以此
表示抽到的汞含量超标的鱼的条数.以此 .
.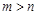 的概率为
的概率为