题目内容
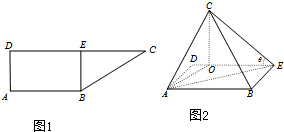 (2012•深圳一模)如图,直角梯形ABCD中,AB∥CD,AD⊥AB,CD=2AB=4,AD=
(2012•深圳一模)如图,直角梯形ABCD中,AB∥CD,AD⊥AB,CD=2AB=4,AD=| 2 |
(1)求证:CO⊥平面ABED;
(2)问∠CEO(记为θ)多大时,三棱锥C-AOE的体积最大?最大值为多少?
分析:(1)通过证明BE⊥DE,BE⊥CE,CE∩DE=E,利用在与平面垂直的判定定理证明CO⊥平面ABED;
(2)利用∠CEO=θ,表示三棱锥C-AOE的体积的表达式,利用二倍角的正弦函数,通过角的我求出表达式的最大值.
(2)利用∠CEO=θ,表示三棱锥C-AOE的体积的表达式,利用二倍角的正弦函数,通过角的我求出表达式的最大值.
解答:解:(1)证明:在直角梯形ABCD中,
CD=2AB,E为CD的中点,
则AB=DE,又AB∥DE,
AD⊥AB,知BE⊥ED.…(1分)
在四棱锥C-ABED中,BE⊥DE,BE⊥CE,CE∩DE=E,
CE,DE?平面CDE,则BE⊥平面CDE.…(3分)
因为CO?平面CDE,所以BE⊥CO…(4分)
又CO⊥DE,且BE,DE是平面ABDE内两条相交直线,…(6分)
故CO⊥平面ABED.…(7分)
(2)解:由(1)知CO⊥平面ABED,
知三棱锥C-AOE的体积V=
S△AOE•OC=
×
×OE×AD×OC…(9分)
由直角梯形ABCD中,CD=2AB=4,AD=
,CE=2,
得三棱锥C-AOE中,
OE=CEcosθ=2cosθ,OC=CEsinθ=2sinθ…(10分)
V=
sin2θ≤
,…(11分)
当且仅当sin2θ=1,θ∈(0,
),即θ=
时取等号,…(12分)
(此时OE=
<DE,O落在线段DE内).
故当θ=
时,三棱锥C-AOE的体积最大,最大值为
.…(13分)
CD=2AB,E为CD的中点,
则AB=DE,又AB∥DE,
AD⊥AB,知BE⊥ED.…(1分)

在四棱锥C-ABED中,BE⊥DE,BE⊥CE,CE∩DE=E,
CE,DE?平面CDE,则BE⊥平面CDE.…(3分)
因为CO?平面CDE,所以BE⊥CO…(4分)
又CO⊥DE,且BE,DE是平面ABDE内两条相交直线,…(6分)
故CO⊥平面ABED.…(7分)
(2)解:由(1)知CO⊥平面ABED,
知三棱锥C-AOE的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
由直角梯形ABCD中,CD=2AB=4,AD=
| 2 |
得三棱锥C-AOE中,
OE=CEcosθ=2cosθ,OC=CEsinθ=2sinθ…(10分)
V=
| ||
| 3 |
| ||
| 3 |
当且仅当sin2θ=1,θ∈(0,
| π |
| 2 |
| π |
| 4 |
(此时OE=
| 2 |
故当θ=
| π |
| 4 |
| ||
| 3 |
点评:本题主要考察空间点、线、面位置关系,棱锥的体积及三角函数等基础知识,考查空间想象能力、运算能力和推理论证能力.

练习册系列答案
相关题目
