题目内容
(2012•深圳一模)如图,平行四边形ABCD中,AB⊥BD,AB=2,BD=
,沿BD将△BCD折起,使二面角A-BD-C是大小为锐角α的二面角,设C在平面ABD上的射影为O.

(1)当α为何值时,三棱锥C-OAD的体积最大?最大值为多少?
(2)当AD⊥BC时,求α的大小.
| 2 |

(1)当α为何值时,三棱锥C-OAD的体积最大?最大值为多少?
(2)当AD⊥BC时,求α的大小.
分析:(1)由题意可得BD⊥OD,可得S△AOD=
OD•BD,OC⊥平面ABDO,利用三棱锥的体积计算公式和正弦函数的单调性即可得出;
(2)建立如图所示的空间直角坐标系,由AD⊥BC,?
•
=0,即可得出.
| 1 |
| 2 |
(2)建立如图所示的空间直角坐标系,由AD⊥BC,?
| AD |
| BC |
解答: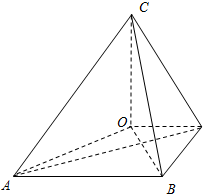 解:(1)由题知OD为CD在平面ABD上的射影,
解:(1)由题知OD为CD在平面ABD上的射影,
∵BD⊥CD,CO⊥平面ABD,∴BD⊥OD,
∴∠ODC=α,则OC=CDsinα,OD=CDcosα.
∴VC-AOD=
S△AOD•OC=
•
•OD•BD•OC
=
•OD•OC=
•CD•sinα•CD•cosα=
•sin2α≤
,
当且仅当sin2α=1,即α=45°时取等号,
∴当α=45°时,三棱锥O-ACD的体积最大,最大值为
.
(2)过O作OE⊥AB于E,则OEBD为矩形,
以O为原点,OE,OD,OC所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则O(0, 0, 0), D(0, 2cosα, 0), A(
, 2cosα-2, 0),
B(
, 2cosα, 0),C(0, 0, 2sinα),
于是
=(-
, 2, 0),
=(-
, -2cosα, 2sinα),
由AD⊥BC,得
•
=0,
∴(-
)×(-
)+2×(-2cosα)+0×2sinα=0,
得cosα=
,又α为锐角,∴α=60°.
 解:(1)由题知OD为CD在平面ABD上的射影,
解:(1)由题知OD为CD在平面ABD上的射影,∵BD⊥CD,CO⊥平面ABD,∴BD⊥OD,
∴∠ODC=α,则OC=CDsinα,OD=CDcosα.
∴VC-AOD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
=
| ||
| 6 |
| ||
| 6 |
| ||
| 3 |
| ||
| 3 |
当且仅当sin2α=1,即α=45°时取等号,
∴当α=45°时,三棱锥O-ACD的体积最大,最大值为
| ||
| 3 |
(2)过O作OE⊥AB于E,则OEBD为矩形,
以O为原点,OE,OD,OC所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则O(0, 0, 0), D(0, 2cosα, 0), A(
| 2 |
B(
| 2 |

于是
| AD |
| 2 |
| BC |
| 2 |
由AD⊥BC,得
| AD |
| BC |
∴(-
| 2 |
| 2 |
得cosα=
| 1 |
| 2 |
点评:本题主要考察空间点、线、面位置关系,棱锥的体积、二面角及三角函数等基础知识,考查空间想象能力、运算能力和推理论证能力,考查用向量方法解决数学问题的能力.

练习册系列答案
相关题目