��Ŀ����
�躯��f��x���Ķ�����ΪR����x��0ʱf��x����1���Ҷ������ʵ��x��y��R����f��x+y��=f��x��f��y��������{an}���� ��
��������f��0����ֵ���жϲ�֤������f��x���ĵ����ԣ�
�����������t��s��N*��s��t��ʹ�õ㣨t��as������s��at������ֱ��y=kx-1�ϣ����ж��Ƿ������Ȼ��M����n��Mʱ��an��0������������ڣ����M����Сֵ���������ڣ���˵�����ɣ�
������a1=f��0��������ʽ
 �Բ�С��2�����������������x��ȡֵ��Χ��
�Բ�С��2�����������������x��ȡֵ��Χ��
���𰸡�����������x��y��R����f��x+y��=f��x��f��y������x��0ʱ����x=-1��y=0�Լ�f��-1����1���Ƴ�f��0��=1�����õ����ԵĶ�����ȡx1��x2 �Ƴ� f��x2��=f��x1+x2-x1��=f��x1��f��x2-x1�����õ�f��x����R�ϼ�������
����ͨ�������ĵ����ԣ��õ�an+1=an+2���㣨t��as������s��at������ֱ��y=kx-1�ϣ��Ƴ�as-at=-2��t-s����ȷ��an=-2��t+s��-1+2n��ͨ����n��Mʱ��a n��f��0����������Ƴ� Ȼ�����M����Сֵ��
Ȼ�����M����Сֵ��
��III�������an��ͨ�ʽ��Ȼ����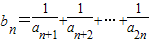 ��֤�����ԣ��Ӷ����bn����Сֵ��ʹ��Сֵ����
��֤�����ԣ��Ӷ����bn����Сֵ��ʹ��Сֵ����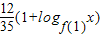 ���Ӷ��������
���Ӷ��������
����⣺����x��y��R��f��x+y��=f��x��•f��y����x��0ʱ��f��x����1
��x=-1��y=0��f��-1��=f��-1��f��0����f��-1����1��f��0��=1����2�֣�
��x��0����f��x-x��=f��0��=f��x��f��-x���� ����3�֣�
����3�֣�
��ȡx1��x2��f��x2��=f��x1+x2-x1��=f��x1��f��x2-x1��
��x2-x1��0��0��f��x2-x1����1��f��x2����f��x1��
��f��x����R�ϼ���������4�֣�
����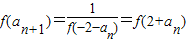 ��f��x�������Եã�an+1=an+2
��f��x�������Եã�an+1=an+2
��{an}�ǵȲ����У�an=a1+2��n-1������5�֣�
�ߴ���t��s��N*��ʹ�ã�t��as���ͣ�s��at������y=kx-1�ϣ�
��as=kt-1����at=ks-1����
��-�ڵ�as-at=k��t-s����
��as=a1+2��s-1����at=a1+2��t-1������as-at=-2��t-s����
��s��t����k=-2����6�֣�
��+�ڣ���as+at=-2��t+s��-2��
��as+at=a1+2��s-1��+a1+2��t-1��
=2a1+2��s+t��-4��
��2a1+2��s+t��-4=-2��t+s��-2
��a1=-2��t+s��+1��0����an=-2��t+s��-1+2n
������{an}������Ϊ��������Ϊ���ĵȲ����У���ȫΪ����������7�֣�
��һ������һ����Ȼ��M��ʹ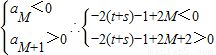
���t+s- ��M��t+s+
��M��t+s+ ��
��
��M��N����M=t+s��
��������Ȼ��M=t+s��ʹ�õ�n��Mʱ��an��0�����������9�֣�
����a1=f��0��=1���ɣ��� an=2n-1
��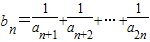 ����
����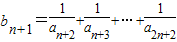 ��
�� =
=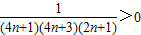 ��
��
��{bn}�ǵ������С���11�֣�
��n��2ʱ��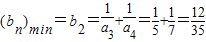 ����12�֣�
����12�֣�
��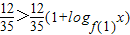
��logf��1��x��0��0��f��1����1����x��ȡֵ��Χ�ǣ�1��+�ޣ�����14�֣�
������������Ҫ�����������뺯���Ĺ�ϵ�����е��жϣ������ĵ����Ե�Ӧ�ã�����ת��˼�룬����������������������������⣮
����ͨ�������ĵ����ԣ��õ�an+1=an+2���㣨t��as������s��at������ֱ��y=kx-1�ϣ��Ƴ�as-at=-2��t-s����ȷ��an=-2��t+s��-1+2n��ͨ����n��Mʱ��a n��f��0����������Ƴ�
 Ȼ�����M����Сֵ��
Ȼ�����M����Сֵ����III�������an��ͨ�ʽ��Ȼ����
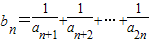 ��֤�����ԣ��Ӷ����bn����Сֵ��ʹ��Сֵ����
��֤�����ԣ��Ӷ����bn����Сֵ��ʹ��Сֵ����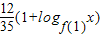 ���Ӷ��������
���Ӷ������������⣺����x��y��R��f��x+y��=f��x��•f��y����x��0ʱ��f��x����1
��x=-1��y=0��f��-1��=f��-1��f��0����f��-1����1��f��0��=1����2�֣�
��x��0����f��x-x��=f��0��=f��x��f��-x����
 ����3�֣�
����3�֣���ȡx1��x2��f��x2��=f��x1+x2-x1��=f��x1��f��x2-x1��
��x2-x1��0��0��f��x2-x1����1��f��x2����f��x1��
��f��x����R�ϼ���������4�֣�
����
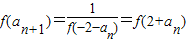 ��f��x�������Եã�an+1=an+2
��f��x�������Եã�an+1=an+2��{an}�ǵȲ����У�an=a1+2��n-1������5�֣�
�ߴ���t��s��N*��ʹ�ã�t��as���ͣ�s��at������y=kx-1�ϣ�
��as=kt-1����at=ks-1����
��-�ڵ�as-at=k��t-s����
��as=a1+2��s-1����at=a1+2��t-1������as-at=-2��t-s����
��s��t����k=-2����6�֣�
��+�ڣ���as+at=-2��t+s��-2��
��as+at=a1+2��s-1��+a1+2��t-1��
=2a1+2��s+t��-4��
��2a1+2��s+t��-4=-2��t+s��-2
��a1=-2��t+s��+1��0����an=-2��t+s��-1+2n
������{an}������Ϊ��������Ϊ���ĵȲ����У���ȫΪ����������7�֣�
��һ������һ����Ȼ��M��ʹ
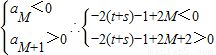
���t+s-
 ��M��t+s+
��M��t+s+ ��
����M��N����M=t+s��
��������Ȼ��M=t+s��ʹ�õ�n��Mʱ��an��0�����������9�֣�
����a1=f��0��=1���ɣ��� an=2n-1
��
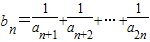 ����
����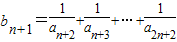 ��
�� =
=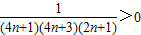 ��
����{bn}�ǵ������С���11�֣�
��n��2ʱ��
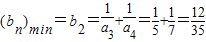 ����12�֣�
����12�֣���
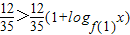
��logf��1��x��0��0��f��1����1����x��ȡֵ��Χ�ǣ�1��+�ޣ�����14�֣�
������������Ҫ�����������뺯���Ĺ�ϵ�����е��жϣ������ĵ����Ե�Ӧ�ã�����ת��˼�룬����������������������������⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ����b=f��
����b=f�� ���Ĵ�С��ϵΪ________��
���Ĵ�С��ϵΪ________�� ����b=f��
����b=f�� ���Ĵ�С��ϵΪ ��
���Ĵ�С��ϵΪ �� ����b=f��
����b=f�� ���Ĵ�С��ϵΪ�� ����
���Ĵ�С��ϵΪ�� ����