题目内容
2．已知函数f（x）=2x-m的图象与函数g（x）=$\frac{x}{2}$-2图象关于直线y=x对称，则m=-4．分析 函数f（x）=2x-m的图象与函数g（x）=$\frac{x}{2}$-2图象关于直线y=x对称，可得函数f（x）=2x-m的图象与函数g（x）=$\frac{x}{2}$-2互为反函数．解出即可．
解答 解：∵函数f（x）=2x-m的图象与函数g（x）=$\frac{x}{2}$-2图象关于直线y=x对称，
∴函数f（x）=2x-m的图象与函数g（x）=$\frac{x}{2}$-2互为反函数．
由g（x）=$\frac{x}{2}$-2=y，解得x=2y+4，
把x与y互换可得：y=2x+4，与f（x）=2x-m=y是同一个函数，
可得-m=4，
解得m=-4．
故答案为：-4．
点评 本题考查了互为反函数的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
12．
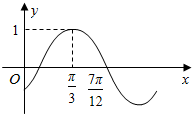已知函数y=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则 （ ）
已知函数y=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则 （ ）| A． | ω=1，φ=$\frac{π}{6}$ | B． | ω=1，φ=-$\frac{π}{6}$ | C． | ω=2，φ=$\frac{π}{6}$ | D． | ω=2，φ=-$\frac{π}{6}$ |
13．函数f（x）=sin（x+$\frac{π}{6}$）的一个递减区间是（ ）
| A． | [-$\frac{π}{2}$，$\frac{π}{2}$] | B． | [-π，0] | C． | [-$\frac{2}{3}π$，$\frac{2}{3}π$] | D． | [$\frac{π}{2}$，$\frac{2}{3}π$] |
16．满足不等式组$\left\{{\begin{array}{l}{3x-2y-2＞0}\\{x+4y+4＞0}\\{2x+y-6＜0}\end{array}}\right.$任意一点（x，y）都使不等式x+y+m≥0恒成立，则实数m的取值范围为（ ）
| A． | （1，+∞） | B． | [1，+∞） | C． | [-2，+∞） | D． | （-∞，4] |