题目内容
7．若实数a，b，c成等差数列，点P（-1，-2）在动直线l：ax+by+c=0上的射影为点M，点N（3，2），则|MN|的最大值为（ ）| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
分析 由于不全为零的实数a，b，c成等差数列，可得2b=a+c．代入直线l：ax+by+c=0可得a（2x+y）+c（y+2）=0．可得：动直线l过定点（1，-2）．由于PM⊥MQ，可知点M在以PQ为直径的圆上，进而得出答案．
解答 
解：∵不全为零的实数a，b，c成等差数列，
∴2b=a+c．把b=$\frac{a+c}{2}$代入直线l：ax+by+c=0可得$ax+\frac{a+c}{2}y+c=0$，
化为a（2x+y）+c（y+2）=0．
由于a，c不全为0，联立$\left\{\begin{array}{l}{2x+y=0}\\{y+2=0}\end{array}\right.$解得$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$，
可知：动直线l过定点Q（1，-2）．
设点M（x，y），
∵PM⊥QM．
∴$\overrightarrow{PM}•\overrightarrow{QM}$=（x+1，y+2）•（x-1，y+2）=x2-1+（y+2）2=0，
化为x2+（y+2）2=1．
因此点M在以（0，-2）为圆心，1为半径的圆上，
圆心（0，-2）到N（3，2）的距离d=$\sqrt{{3}^{2}+（-2-2）^{2}}=\sqrt{9+16}$=$\sqrt{25}$=5，
则|MN|的最大值为d+r=5+1=6．
故选：B．
点评 本题考查了等差数列的定义、直线系过定点问题、圆的标准方程及其性质、最值问题等基础知识与基本技能方法，属于难题．综合性较强．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
18．（2x-$\frac{1}{x}$）4的展开式中的常数项为（ ）
| A． | 6 | B． | -6 | C． | 24 | D． | -24 |
15．下列不等式中恒成立的是（ ）
| A． | $2-x-\frac{4}{x}$≤-2 | B． | $sinx+\frac{1}{sinx}$≥2 | C． | $\frac{{{x^2}+5}}{{\sqrt{{x^2}+4}}}$≥2 | D． | $\frac{{{x^2}+2}}{{\sqrt{{x^2}+2}}}$≥$\sqrt{2}$ |
19．某地区2009年至2013年农村居民家庭人均纯收入y（单位：千元）的数据如下表：
（1）用最小二乘法求y关于x的线性回归方程；
（2）利用（1）中的回归方程，分析2009年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入．
| 年份 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号x | 1 | 2 | 3 | 4 | 5 |
| 人均纯收入y | 2.8 | 3.2 | 4.2 | 4.8 | 5 |
（2）利用（1）中的回归方程，分析2009年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入．
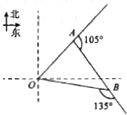如图，一只蜘蛛从点O出发沿北偏东45°方向爬行xcm，到达点A处捕捉到一只小虫，然后沿OA方向右转105°爬行10cm，到达点B处捕捉哦另一只小虫，这时他沿AB方向右转135°爬行回到它的出发点O处，那么x=$\frac{10\sqrt{6}}{3}$．