题目内容
【题目】在△ABC中,已知tanA,tanB是关于x的方程x2+(x+1)p+1=0的两个实根.
(1)求角C;
(2)求实数p的取值集合.
【答案】
(1)解:根据题意,则有tanA+tanB=﹣p,tanAtanB=p+1,
而 ![]() ,又A,B是△ABC的内角,
,又A,B是△ABC的内角,
所以 ![]() ,则
,则 ![]() .
.
(2)解:在△ABC中由(1)知 ![]() ,则
,则 ![]() ,即tanA,tanB∈(0,1),…(6分)
,即tanA,tanB∈(0,1),…(6分)
则关于x的方程x2+(p+1)x+1=x2+px+p+1=0在区间(0,1)上有两个实根,
设f(x)=x2+px+p+1,则函数f(x)与x轴有两个交点,且交点在(0,1)内;
又函数f(x)的图象是开口向上的抛物线,且对称轴方程为x=﹣ ![]() ,
,
故其图象满足: 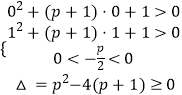 ,
,
解之得: ![]() .
.
所以实数p的取值集合为 ![]() .
.
【解析】(1)先由根系关系得出tanA与tanB和与积,由正切的和角公式代入求值,结合A,B的范围即可计算得解A+B的值,利用三角形内角和定理即可求C的值.(2)由(1)可求A,B的取值范围,进而得方程两根的取值范围,构造函数f(x)=x2+px+p+1,则函数的两个零点均在区间(0,1)内,利用二次函数的性质构造关于p的不等式组可以求出满足条件的p的范围.
【考点精析】本题主要考查了两角和与差的正切公式的相关知识点,需要掌握两角和与差的正切公式:![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目