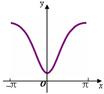
题目内容
已知周期函数 的定义域为
的定义域为 ,周期为2,且当
,周期为2,且当 时,
时, .若直线
.若直线 与曲线
与曲线 恰有2个交点,则实数
恰有2个交点,则实数 的所有可能取值构成的集合为( )
的所有可能取值构成的集合为( )
A. 或 或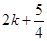   | B. 或 或   |
C. 或 或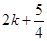   | D.   |
C
解析试题分析:对于直线 ,
, 可视为直线
可视为直线 在
在 轴上的恒截距,如下图所示,当
轴上的恒截距,如下图所示,当 时,当直线
时,当直线 与函数
与函数 相切时,直线
相切时,直线 在曲线
在曲线 在区间
在区间 上还有一个交点,即此时函数
上还有一个交点,即此时函数 与曲线
与曲线 有两个交点,当
有两个交点,当 ,
, ,则
,则 ,
,
令 ,解得
,解得 ,
, ,切点坐标为
,切点坐标为 ,故有
,故有 ,
,
解得 ,将此直线向左或向右每次平移
,将此直线向左或向右每次平移 个单位长度,所得到的直线与曲线
个单位长度,所得到的直线与曲线 仍有两个公共点,此时
仍有两个公共点,此时 ;当直线
;当直线 过点
过点 ,此时直线
,此时直线 与曲线
与曲线 还有一个公共点,此时有
还有一个公共点,此时有 ,解得
,解得 ,将此直线向左或向右每次平移
,将此直线向左或向右每次平移 个单位长度,所得到的直线与曲线
个单位长度,所得到的直线与曲线 仍有两个公共点,此时
仍有两个公共点,此时 .综上所述,实数
.综上所述,实数 所有可能取值的集合对应选项为C.
所有可能取值的集合对应选项为C.
考点:函数的周期性、函数的零点

练习册系列答案
相关题目
若定义在R上的偶函数 满足
满足 且
且 时,
时, 则方程
则方程 的零点个数是( )
的零点个数是( )
| A. 2个 | B. 3个 | C.4个 | D.多于4个 |
下列函数中,既是偶函数又在区间 上单调递增的函数为( )
上单调递增的函数为( )
A. | B. | C. | D. |
函数 所有零点的和等于( )
所有零点的和等于( )
| A.6 | B.7.5 | C.9 | D.12 |
已知函数 对于任意的
对于任意的 ,导函数
,导函数 都存在,且满足
都存在,且满足 ≤0,则必有( )
≤0,则必有( )
A. > > | B. ≤ ≤ |
C. < < | D. ≥ ≥ |
已知f(x)是实数集上的偶函数,且在区间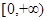 上是增函数,则
上是增函数,则 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |
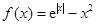 的图象是 ( )
的图象是 ( )

 与
与 和区间D,如果存在
和区间D,如果存在 ,使
,使 ,则称
,则称 是函数
是函数 ,
, ②
② ,
,
 ,
, ④
④ ,
,
 上存在“友好点”的有( )
上存在“友好点”的有( ) 的大致图象为( )
的大致图象为( )