题目内容
5. 如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.(1)求证:A1B∥面ADC1;
(2)求直线B1C1与平面ADC1所成角的余弦值.
分析 (1)建立空间直角坐标系,求出平面ADC1的法向量,证明$\overrightarrow{{A_1}B}•\overrightarrow m=2×2+0×({-2})+({-4})×1=0$,即可证明A1B∥面ADC1;
(2)求出:$\overrightarrow{{B_1}{C_1}}=({-2,2,0})$,利用向量的夹角公式,即可求直线B1C1与平面ADC1所成角的余弦值.
解答  (1)证明:如图,以{$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{A{A}_{1}}$}为单位正交基底建立空间直角坐标系A-xyz,
(1)证明:如图,以{$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{A{A}_{1}}$}为单位正交基底建立空间直角坐标系A-xyz,
则A(0,0,0),B(2,0,0),C(0,2,0),A1(0,0,4),D(1,1,0),B1(2,0,4),C1(0,2,4)
∴$\overrightarrow{{A_1}B}=(2,0,-4)$,$\overrightarrow{AD}=(1,1,0)$,$\overrightarrow{A{C_1}}=(0,2,4)$,
设平面ADC1的法向量为$\overrightarrow m=(x,y,z)$,由$\overrightarrow m⊥\overrightarrow{AD},\overrightarrow m⊥\overrightarrow{A{C_1}}$
∴$\left\{\begin{array}{l}x+y=0\\ 2y+4z=0\end{array}\right.$取z=1,得y=-2,x=2,∴平面ADC1的法向量为$\overrightarrow m=(2,-2,1)$
由此可得,$\overrightarrow{{A_1}B}•\overrightarrow m=2×2+0×({-2})+({-4})×1=0$,
又A1B?平面ADC1,
∴A1B∥面ADC1.
(2)解:$\overrightarrow{{B_1}{C_1}}=({-2,2,0})$,设直线B1C1与平面ADC1所成角为θ,则$sinθ=|{cos<\overrightarrow{{B_1}{C_1}},\overrightarrow m>}|=\frac{{|{\overrightarrow{{B_1}{C_1}}•\overrightarrow m}|}}{{|{\overrightarrow{{B_1}{C_1}}}||{\overrightarrow m}|}}=\frac{{2\sqrt{2}}}{3}$,
又θ为锐角,
∴直线B1C1与平面ADC1所成角的余弦值为$\frac{1}{3}$.
点评 本题考查线面平行,考查直线B1C1与平面ADC1所成角的余弦值,考查学生分析解决问题的能力,正确运用向量法是关键,属于中档题.

| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
| A. | [-2015,2015] | B. | [-2014,2016] | ||
| C. | (-∞,2014]∪[2016,+∞) | D. | (-∞,-2016]∪[2014,+∞) |
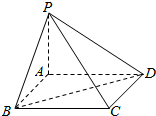 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,若AP=1,AD=$\sqrt{3}$,三棱锥P-ABD的体积V=$\frac{\sqrt{3}}{4}$,则A到平面PBC的距离是$\frac{3\sqrt{13}}{13}$.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,若AP=1,AD=$\sqrt{3}$,三棱锥P-ABD的体积V=$\frac{\sqrt{3}}{4}$,则A到平面PBC的距离是$\frac{3\sqrt{13}}{13}$.