Question

已知A，B是抛物线y²=2px（p＞0）上两点，O为坐标原点，若|OA|=|OB|，且△AOB的垂心恰好是此抛物线的焦点，则直线AB的方程是（　　）

• A．x=p
• B．x=3p
• C．x=

  3

  2

  p
• D．x=

  5

  2

  p

Answer 1

分析：由抛物线的对称性知A、B关于x轴对称，设出它们的坐标，利用三角形的垂心的性质，结合斜率之积等于-1，求出A、B坐标即可解决．

解答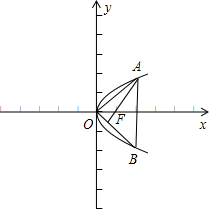：解：由A、B是抛物线y²=2px（p＞0）的两点，|AO|=|BO|，
及抛物线的对称性知，A、B关于x轴对称．
设直线AB的方程是 x=m，则  A（ m，

2pm

）、B（m，-

2pm

）
|△AOB的垂心恰好是抛物线的焦点F（

p

2

，0 ）
∴AF⊥OB，K_AF•K_OB=-1，
∴

2pm -0

m- p 2

•

- 2pm -0

m-0

=-1
∴m=

5p

2

，∴直线AB的方程是 x=

5p

2

故选D．

点评：本小题主要考查抛物线的简单性质、三角形垂心性质等基础知识，考查运算求解能力，考查数形结合思想与转化思想．属于基础题．