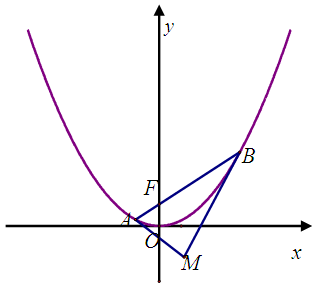
题目内容
已知动圆经过点 ,且和直线
,且和直线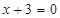 相切,
相切,
(1)求动圆圆心的轨迹C的方程;
(2)已知曲线C上一点M,且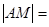 5,求M点的坐标.
5,求M点的坐标.
(1) 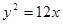 ; (2)
; (2) 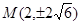
解析试题分析:根据题意可知,动圆圆心到点A的距离与到直线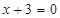 的距离相等,所以动圆圆心的轨迹满足抛物线的定义,其轨迹为以A为焦点,直线
的距离相等,所以动圆圆心的轨迹满足抛物线的定义,其轨迹为以A为焦点,直线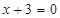 为准线的抛物线;由抛物线的定义和几何性质可知,点M到焦点的距离等于其到准线的距离,即可得到点M的坐标.
为准线的抛物线;由抛物线的定义和几何性质可知,点M到焦点的距离等于其到准线的距离,即可得到点M的坐标.
试题解析:(1)由题意,动圆圆心到点A的距离与到直线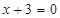 的距离相等,所以动圆圆心的轨迹为A为焦点,以
的距离相等,所以动圆圆心的轨迹为A为焦点,以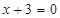 为准线的抛物线,其方程为
为准线的抛物线,其方程为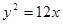 ;
;
(2)设M的坐标为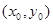 ,由题意知
,由题意知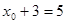 ,所以
,所以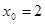 ;代入抛物线方程得,
;代入抛物线方程得,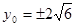 ,所以
,所以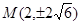
考点:本题主要考察了抛物线的定义和几何性质的应用.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
 及
及 ,点
,点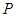 在以
在以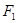 、
、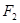 为焦点的椭圆
为焦点的椭圆 上,且
上,且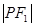 、
、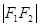 、
、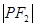 构成等差数列.
构成等差数列.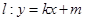 与椭圆
与椭圆 是直线
是直线 上的两点,且
上的两点,且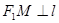 ,
,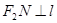 . 求四边形
. 求四边形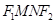 面积
面积 的最大值.
的最大值.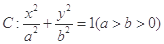 的离心率为
的离心率为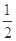 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线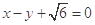 相切,过点P(4,0)且不垂直于x轴直线
相切,过点P(4,0)且不垂直于x轴直线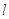 与椭圆C相交于A、B两点.
与椭圆C相交于A、B两点. 的取值范围;
的取值范围; :
: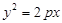 和⊙
和⊙ :
: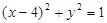 ,过抛物线
,过抛物线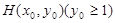 作两条直线与⊙
作两条直线与⊙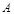 、
、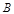 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点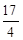 .
.
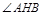 的角平分线垂直
的角平分线垂直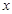 轴时,求直线
轴时,求直线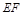 的斜率;
的斜率;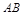 在
在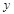 轴上的截距为
轴上的截距为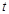 ,求
,求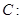
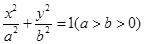 的离心率为
的离心率为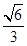 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为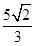 .
. 的方程;
的方程;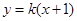 与椭圆
与椭圆 、
、 两点. ①若线段
两点. ①若线段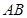 中点的横坐标为
中点的横坐标为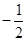 ,求斜率
,求斜率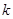 的值;②若点
的值;②若点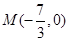 ,求证:
,求证: 为定值.
为定值. +
+ =1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°
=1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°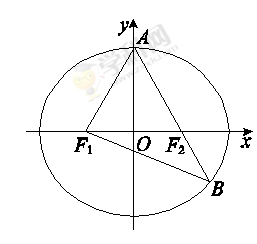
 ,求a,b的值
,求a,b的值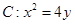 的焦点为
的焦点为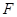 ,过点
,过点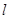 交抛物线
交抛物线 于
于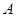 、
、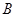 两点,经过
两点,经过 、
、 ,切线
,切线 .
.
 在第二象限,且到准线距离为
在第二象限,且到准线距离为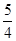 时,求
时,求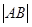 ;
;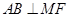 .
. 中,已知圆
中,已知圆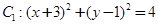 和圆
和圆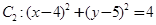 .
. 过点
过点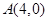 ,且被圆
,且被圆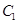 截得的弦长为
截得的弦长为 ,求直线
,求直线 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点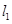 和
和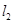 ,它们分别与圆
,它们分别与圆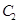 相交,且直线
相交,且直线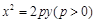 相交于B、C,当直线l的斜率是
相交于B、C,当直线l的斜率是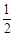 时,
时,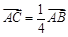 .
.