题目内容
如图,已知抛物线 :
: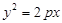 和⊙
和⊙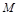 :
: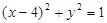 ,过抛物线
,过抛物线 上一点
上一点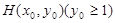 作两条直线与⊙
作两条直线与⊙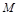 相切于
相切于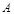 、
、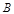 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点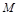 到抛物线准线的距离为
到抛物线准线的距离为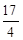 .
.
(1)求抛物线 的方程;
的方程;
(2)当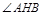 的角平分线垂直
的角平分线垂直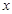 轴时,求直线
轴时,求直线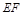 的斜率;
的斜率;
(3)若直线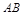 在
在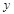 轴上的截距为
轴上的截距为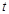 ,求
,求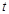 的最小值.
的最小值.
(1)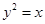 ;(2)
;(2) ;(3)
;(3)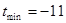 .
.
解析试题分析:本题考查抛物线、圆的标准方程以及直线与抛物线、圆的位置关系,突出解析几何的基本思想和方法的考查:如数形结合思想、坐标化方法等.第一问,据点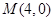 到准线
到准线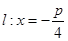 的距离为
的距离为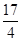 ,直接列式求得
,直接列式求得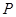 ,得到抛物线的标准方程;第二问,据条件
,得到抛物线的标准方程;第二问,据条件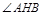 的角平分线为
的角平分线为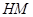 ,即
,即 轴,得
轴,得 ,而
,而 ,
,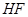 关于
关于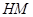 对称,所以
对称,所以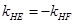 ,利用两点斜率公式代入得
,利用两点斜率公式代入得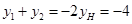 ,所以求得
,所以求得 ;第三问,先求直线
;第三问,先求直线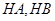 的方程,再求
的方程,再求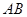 的方程,令
的方程,令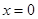 ,可得到
,可得到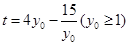 ,利用函数的单调性求函数的最值.
,利用函数的单调性求函数的最值.
试题解析:(1)∵点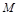 到抛物线准线的距离为
到抛物线准线的距离为
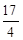 ,
,
∴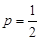 ,即抛物线
,即抛物线 的方程为
的方程为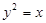 .
.
(2)法一:∵当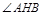 的角平分线垂直
的角平分线垂直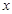 轴时,点
轴时,点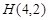 ,∴
,∴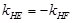 ,
,
设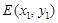 ,
,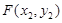 ,
,
∴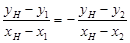 , ∴
, ∴ 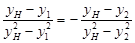 ,
,
∴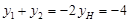 .
.  .
.
法二:∵当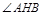 的角平分线垂直
的角平分线垂直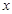 轴时,点
轴时,点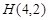 ,∴
,∴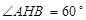 ,可得
,可得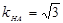 ,
,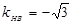 ,∴直线
,∴直线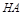 的方程为
的方程为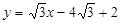 ,
,
联立方程组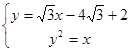 ,得
,得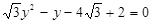 ,
,
∵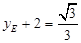 ∴
∴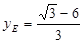 ,
,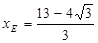 .
.
同理可得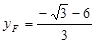 ,
,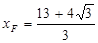 ,∴
,∴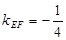 .
.
(3)法一:设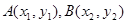 ,∵
,∵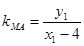 ,∴
,∴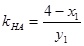 ,
,
可得,直线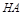 的方程为
的方程为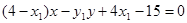 ,
,
同理,直线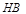 的方程为
的方程为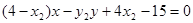 ,
,
∴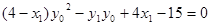 ,
,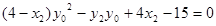 ,
,
∴直线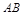 的方程为
的方程为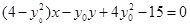 ,
,
令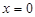 ,可得
,可得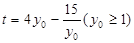 ,
,
∵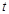 关于
关于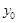 的函数在
的函数在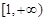 单调递增, ∴
单调递增, ∴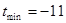 .
.
法二:设点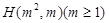 ,
,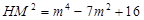 ,
,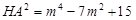 .
.
以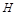 为圆心,
为圆心, 为半径的圆方程为
为半径的圆方程为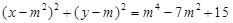

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
 的中心为直角坐标系
的中心为直角坐标系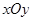 的原点,焦点在
的原点,焦点在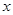 轴上,它的一个顶点到两个焦点的距离分别是7和1.
轴上,它的一个顶点到两个焦点的距离分别是7和1.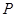 为椭圆
为椭圆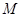 为过
为过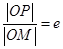 (
(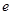 为椭圆的离心率),求点
为椭圆的离心率),求点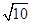 时,求k的值.
时,求k的值. 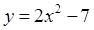 ,求曲线过点
,求曲线过点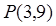 的切线方程。
的切线方程。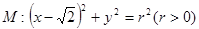 ,若椭圆
,若椭圆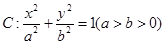 的右顶点为圆
的右顶点为圆 的圆心,离心率为
的圆心,离心率为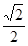 .
. 的方程;
的方程;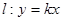 ,使得直线
,使得直线 与椭圆
与椭圆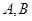 两点,与圆
两点,与圆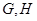 两点,点
两点,点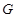 在线段
在线段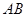 上,且
上,且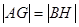 ,求圆
,求圆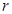 的取值范围.
的取值范围. ,且和直线
,且和直线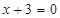 相切,
相切,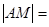 5,求M点的坐标.
5,求M点的坐标.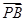 |,
|, |
|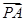 |,8成等差数列.
|,8成等差数列.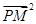 ,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?
,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?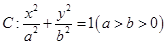 过点
过点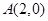 ,离心率为
,离心率为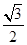 .
.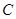 的方程;
的方程;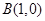 且斜率为
且斜率为 (
(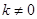 )的直线
)的直线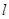 与椭圆
与椭圆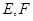 两点,直线
两点,直线 、
、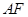 分别交直线
分别交直线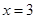 于
于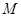 、
、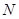 两点,线段
两点,线段 的中点为
的中点为 .记直线
.记直线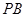 的斜率为
的斜率为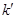 ,求证:
,求证: 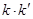 为定值.
为定值.