题目内容
下列函数中,既是偶函数又在区间(1,2)上单调递增的是( )
A.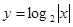
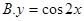
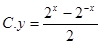
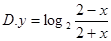
A
解析试题分析: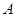 与
与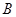 满足
满足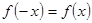 ,
, 与
与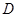 满足
满足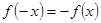 ,为奇函数,所以舍去,画出
,为奇函数,所以舍去,画出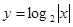 与
与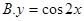 的图象
的图象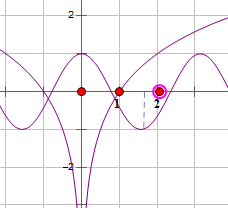
显然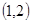 递增的是
递增的是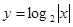 ,故选A.
,故选A.
考点:1.函数的奇偶性;2.函数的单调性;3.函数的图象.

练习册系列答案
相关题目
方程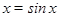 的解个数为( )
的解个数为( )
A.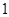 | B.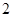 | C.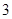 | D.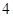 |
用min{a,b)表示a,b两数中的最小值.若函数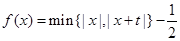 恰有三个零点,则t的值为( ).
恰有三个零点,则t的值为( ).
| A.-2 | B.2 | C.2或-2 | D.1或-l |
函数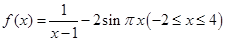 所有零点之和等于 ( ).
所有零点之和等于 ( ).
| A.2 | B.4 | C.6 | D.8 |
函数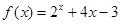 的零点所在区间是( )
的零点所在区间是( )
A.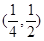 | B.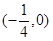 | C.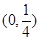 | D.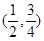 |
设函数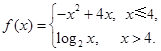 若函数
若函数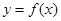 在区间
在区间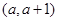 上单调递增,则实数
上单调递增,则实数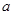 的取值范围是( )
的取值范围是( )
A.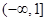 | B.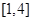 |
C.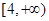 | D.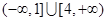 |
对于实数x,符号[x]表示不超过x的最大整数.例如,[π]=3,[-1.08]=-2.如果定义函数f(x)=x-[x],那么下列命题中正确的一个是( )
| A.f(5)=1 |
B.方程f(x)=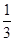 有且仅有一个解 有且仅有一个解 |
| C.函数f(x)是周期函数 |
| D.函数f(x)是减函数 |
[2013·吉林调研]已知定义在R上的函数f(x)满足f(x)+f(-x)=0,且在(-∞,0)上单调递增,如果x1+x2<0且x1x2<0,则f(x1)+f(x2)的值( )
| A.可能为0 | B.恒大于0 |
| C.恒小于0 | D.可正可负 |
设f(x)是定义在实数集R上的函数,满足条件y=f(x+1)是偶函数,且当x≥1时,f(x)=( )x-1,则f(
)x-1,则f( ),f(
),f( ),f(
),f( )的大小关系是 ( )
)的大小关系是 ( )
A.f( )>f( )>f( )>f( )>f( ) ) |
B.f( )>f( )>f( )>f( )>f( ) ) |
C.f( )>f( )>f( )>f( )>f( ) ) |
D.f( )>f( )>f( )>f( )>f( ) ) |