题目内容
证明:在复数范围内,方程|z|2+(1-i)
思路解析:将已知条件化简后再由复数相等来解.
解:原方程化简为|z|2+(1-i)![]() -(1+i)z=1-3i.
-(1+i)z=1-3i.
设z=x+yi(x、y∈R),代入上述方程得x2+y2-2xi-2yi=1-3i.
∴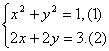
将(2)代入(1),整理得8x2-12x+5=0.
∵Δ=-16<0,∴方程f(x)无实数解.∴原方程在复数范围内无解.
方法归纳 注意此处空半格复数相等是解决复数问题常用的方法,这是一个将复数问题实数化的过程,转化后再用实数范围内的相关方法来解.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
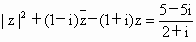 (i为虚数单位)无解.
(i为虚数单位)无解.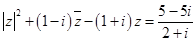 (
(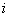 为虚数单位)无解.
为虚数单位)无解.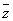 -(1+i)z=
-(1+i)z=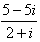 (i为虚数单位)无解。
(i为虚数单位)无解。