题目内容
18、证明:在复数范围内,方程
18.[证明]原方程化简为|z|2+(1-i)![]() -(1+i)z=1-3i.
-(1+i)z=1-3i.
设z=x+yi (x、y∈R),代入上述方程得
x2+y2-2xi-2yi=1-3i
∴ 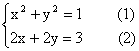
将(2)代入(1),整理得8x2-12x+5=0, (*)
∵△=-16<0, ∴方程(*)无实数解。
∴原方程在复数范围内无解。

练习册系列答案
相关题目
题目内容
18、证明:在复数范围内,方程
18.[证明]原方程化简为|z|2+(1-i)![]() -(1+i)z=1-3i.
-(1+i)z=1-3i.
设z=x+yi (x、y∈R),代入上述方程得
x2+y2-2xi-2yi=1-3i
∴ 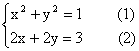
将(2)代入(1),整理得8x2-12x+5=0, (*)
∵△=-16<0, ∴方程(*)无实数解。
∴原方程在复数范围内无解。
