题目内容
10．如图所示，在四边形ABCD中，$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$，试判断四边形的形状．
分析 由向量加法的三角形法则可知$\overrightarrow{AC}$=$\overrightarrow{AD}$+$\overrightarrow{DC}$，结合已知条件$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$可知$\overrightarrow{DC}$=$\overrightarrow{AB}$，故AB=CD，AB∥CD，得出四边形为平行四边形．
解答 解：∵$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$，$\overrightarrow{AC}$=$\overrightarrow{AD}$+$\overrightarrow{DC}$，
∴$\overrightarrow{DC}$=$\overrightarrow{AB}$，
∴AB=CD，AB∥CD，
∴四边形ABCD为平行四边形．
点评 本题考查了平面向量加法的几何意义，是基础题．
练习册系列答案
相关题目
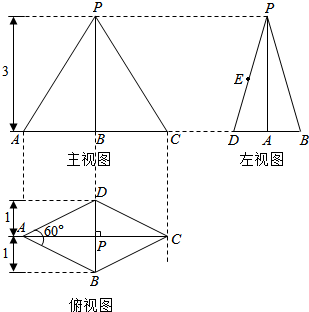一个四棱锥的三视图和直观图如图所示，E为侧棱PD的中点．