题目内容
5.已知y=f(x)是R上的偶函数,且当x∈[0,+∞)时,f(x)=2x-3,则满足f(x)<0的x的取值范围是-log23<x<log23.分析 由偶函数的定义和运用导数判断函数在[0,+∞)上的单调性,可将f(x)<0转化为f(|x|)<f(log23),化简为|x|<log23,即可得到x的取值范围.
解答 解:∵函数f(x)是定义在R上的偶函数,
∴f(-x)=f(x),
∵当x∈[0,+∞)时,f(x)=2x-3,
∴f′(x)=2xln2>0,
∴f(x)在[0,+∞)上单调递增,
又f(log23)=0
∴f(x)<0转化为f(|x|)<f(log23)
∵f(x)在[0,+∞)上单调递增,
∴|x|<log23
∴-log23<x<log23.
故答案为:-log23<x<log23.
点评 本题考查函数的性质及运用,考查函数的奇偶性、单调性及运用,注意函数的定义域,注意运用导数判断单调性,属于中档题.

练习册系列答案
相关题目
15.某数学老师身高179cm,他爷爷、父亲和儿子的身高分别是176cm、173cm和185cm,因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测孙子的身高,已知父亲与儿子身高如表一:
该数学老师提供了三种求回归直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的方案(每种方案都正确).$\stackrel{∧}{b}$=$\frac{\sum_{\;}^{\;}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{\;}^{\;}{x}_{i}^{2}-{n\overline{x}}^{2}}$(公式1),$\stackrel{∧}{b}$=$\frac{\sum_{\;}^{\;}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{\;}^{\;}(x{{\;}_{i}-\overline{x}}^{2})}$(公式2);$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$(公式3)
(方案一):借助(公式1)求$\stackrel{∧}{b}$,借助(公式3),求$\stackrel{∧}{a}$,进而求回归直线方程;
(方案二):借助(公式2)求$\stackrel{∧}{b}$,借助(公式3)求$\stackrel{∧}{a}$,进而求回归直线方程;
(方案三):令X=x-173,Y=y-179,则(表一)转化成诶面的(表二).
借助(表二)和(公式1)、(公式3),求出$\stackrel{∧}{Y}$=$\stackrel{∧}{b}$X+$\stackrel{∧}{a}$,进而求出y对x的回归直线(y-179)=$\stackrel{∧}{b}$(x-173)+$\stackrel{∧}{a}$.
结合数据特点任选一种方案,求y与x的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并根据回归直线预测数学教师的孙子的身高.
| 父亲身高x(cm) | 176 | 173 | 179 |
| 儿子身高y(cm) | 173 | 179 | 185 |
(方案一):借助(公式1)求$\stackrel{∧}{b}$,借助(公式3),求$\stackrel{∧}{a}$,进而求回归直线方程;
(方案二):借助(公式2)求$\stackrel{∧}{b}$,借助(公式3)求$\stackrel{∧}{a}$,进而求回归直线方程;
(方案三):令X=x-173,Y=y-179,则(表一)转化成诶面的(表二).
| X | 3 | 0 | 6 |
| Y | -6 | 0 | 6 |
结合数据特点任选一种方案,求y与x的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并根据回归直线预测数学教师的孙子的身高.
20.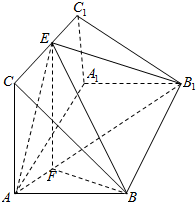 如图,是直三棱柱ABC-A1B1C1中,AA1=6,AB=AC=4,AB⊥AC,点E,F分别是AB1,CC1动点,$\overrightarrow{AF}$=λ$\overrightarrow{F{B}_{1}}$,$\overrightarrow{CE}$=μ$\overrightarrow{E{C}_{1}}$.则当V${\;}_{三棱锥{B}_{1}-EFB}$=4时,必有( )
如图,是直三棱柱ABC-A1B1C1中,AA1=6,AB=AC=4,AB⊥AC,点E,F分别是AB1,CC1动点,$\overrightarrow{AF}$=λ$\overrightarrow{F{B}_{1}}$,$\overrightarrow{CE}$=μ$\overrightarrow{E{C}_{1}}$.则当V${\;}_{三棱锥{B}_{1}-EFB}$=4时,必有( )
 如图,是直三棱柱ABC-A1B1C1中,AA1=6,AB=AC=4,AB⊥AC,点E,F分别是AB1,CC1动点,$\overrightarrow{AF}$=λ$\overrightarrow{F{B}_{1}}$,$\overrightarrow{CE}$=μ$\overrightarrow{E{C}_{1}}$.则当V${\;}_{三棱锥{B}_{1}-EFB}$=4时,必有( )
如图,是直三棱柱ABC-A1B1C1中,AA1=6,AB=AC=4,AB⊥AC,点E,F分别是AB1,CC1动点,$\overrightarrow{AF}$=λ$\overrightarrow{F{B}_{1}}$,$\overrightarrow{CE}$=μ$\overrightarrow{E{C}_{1}}$.则当V${\;}_{三棱锥{B}_{1}-EFB}$=4时,必有( )| A. | λ=$\frac{1}{3}$ | B. | μ=$\frac{1}{3}$ | C. | λ=3 | D. | μ=3 |
8.函数f(x)=$\sqrt{3}$sinx-cosx(x∈[0,π])的单调递减区间是( )
| A. | [0,$\frac{2π}{3}$] | B. | [$\frac{π}{2}$,$\frac{2π}{3}$] | C. | [$\frac{2π}{3}$,π] | D. | [$\frac{π}{2}$,$\frac{5π}{6}$] |
