题目内容
【题目】已知抛物线C:y=(x+1)2与圆 ![]() (r>0)有一个公共点A,且在A处两曲线的切线为同一直线l.
(r>0)有一个公共点A,且在A处两曲线的切线为同一直线l.
(1)求r;
(2)设m,n是异于l且与C及M都相切的两条直线,m,n的交点为D,求D到l的距离.
【答案】
(1)
解:设A(x0,(x0+1)2),
∵y=(x+1)2,y′=2(x+1)
∴l的斜率为k=2(x0+1)
当x0=1时,不合题意,所以x0≠1
圆心M(1, ![]() ),MA的斜率
),MA的斜率 ![]() .
.
∵l⊥MA,∴2(x0+1)× ![]() =﹣1
=﹣1
∴x0=0,∴A(0,1),
∴r=|MA|= ![]() ;
;
(2)
解:设(t,(t+1)2)为C上一点,则在该点处的切线方程为y﹣(t+1)2=2(t+1)(x﹣t),即y=2(t+1)x﹣t2+1
若该直线与圆M相切,则圆心M到该切线的距离为 ![]()
∴ ![]()
∴t2(t2﹣4t﹣6)=0
∴t0=0,或t1=2+ ![]() ,t2=2﹣
,t2=2﹣ ![]()
抛物线C在点(ti,(ti+1)2)(i=0,1,2)处的切线分别为l,m,n,其方程分别为
y=2x+1①,y=2(t1+1)x﹣ ![]() ②,y=2(t2+1)x﹣
②,y=2(t2+1)x﹣ ![]() ③
③
②﹣③:x= ![]()
代入②可得:y=﹣1
∴D(2,﹣1),
∴D到l的距离为 ![]()
【解析】(1)设A(x0 , (x0+1)2),根据y=(x+1)2 , 求出l的斜率,圆心M(1, ![]() ),求得MA的斜率,利用l⊥MA建立方程,求得A的坐标,即可求得r的值;(2)设(t,(t+1)2)为C上一点,则在该点处的切线方程为y﹣(t+1)2=2(t+1)(x﹣t),即y=2(t+1)x﹣t2+1,若该直线与圆M相切,则圆心M到该切线的距离为
),求得MA的斜率,利用l⊥MA建立方程,求得A的坐标,即可求得r的值;(2)设(t,(t+1)2)为C上一点,则在该点处的切线方程为y﹣(t+1)2=2(t+1)(x﹣t),即y=2(t+1)x﹣t2+1,若该直线与圆M相切,则圆心M到该切线的距离为 ![]() ,建立方程,求得t的值,求出相应的切线方程,可得D的坐标,从而可求D到l的距离.
,建立方程,求得t的值,求出相应的切线方程,可得D的坐标,从而可求D到l的距离.
【考点精析】掌握点到直线的距离公式是解答本题的根本,需要知道点![]() 到直线
到直线![]() 的距离为:
的距离为: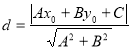 .
.

 阅读快车系列答案
阅读快车系列答案