Question

如图所示，水平地面上有一个大球，现作如下方法测量球的大小：用一个锐角为60⁰的三角板，斜边紧靠球面，一条直角边紧靠地面，并使三角板与地面垂直，P为三角板与球的切点，如果测得PA＝5，则球的表面积为____________

Answer 1

300π.

解析试题分析：连接OA，∵AB与AD都为圆O的切线，
∴∠OPA=90°，∠ODA=90°，
∵∠BAC=60°，∴∠PAD=120°，
∵PA、AD都是⊙O的切线，∴∠OAP=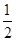∠PAD=60°，
在Rt△OPA中，PA=5cm，tan60°=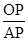，则OP=APtan60°=5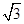cm，即⊙O的半径R为5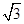cm．
则球的表面积S=4πR²=4π•(5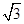)²=300π．
故答案为300π
考点：本题主要考查圆的切线的性质，切线长定理，直角三角形中的边角关系。
点评：中档题，一般地，见了有切线，应把圆心切点连，构造直角三角形解决问题，其中切线长定理为：经过圆外一点引圆的两条切线，切线长相等，且此点与圆心地连线平分两切线的夹角，灵活运用此定理是本题的突破点．