题目内容
直线 相离,若
相离,若 能表示为某三角形的三条边长,则根据已知条件能够确定该三角形的形状是____________.
能表示为某三角形的三条边长,则根据已知条件能够确定该三角形的形状是____________.
钝角三角形
解析试题分析: 因为直线 相离,那么根据点到直线的距离公式可知,
相离,那么根据点到直线的距离公式可知,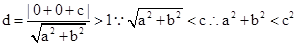 ,由此结合三角形的余弦定理可知,
,由此结合三角形的余弦定理可知,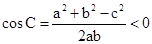 ,可知该三角形为钝角三角形。答案为钝角三角形。
,可知该三角形为钝角三角形。答案为钝角三角形。
考点:本题主要考查了直线与圆的位置关系的运用,以及姐三角形问题。
点评:解决该试题的关键是利用点到直线的距离公式得到a,b,c,的关系式,进而利用余弦定理来判定三角形的形状。

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
已知圆M:(x+cosq)2+(y-sinq)2=1,直线l:y=kx,下面四个命题:
| A.对任意实数k与q,直线l和圆M相切; |
| B.对任意实数k与q,直线l和圆M有公共点; |
| C.对任意实数q,必存在实数k,使得直线l与和圆M相切; |
| D.对任意实数k,必存在实数q,使得直线l与和圆M相切 |
 与圆
与圆 交于不同的两点A、B,O是坐标原点,且
交于不同的两点A、B,O是坐标原点,且 ,则实数m的取值范围是 。
,则实数m的取值范围是 。
 上有且只有两个点到直线
上有且只有两个点到直线 的距离为1,则半径
的距离为1,则半径 的取值范围是 .
的取值范围是 . 上的点到直线
上的点到直线 的最小距离是 .
的最小距离是 .  与⊙
与⊙ 相交于
相交于 两点,且两圆在点
两点,且两圆在点 处的切线互相垂直,则线段
处的切线互相垂直,则线段 的长度是
的长度是 
 关于直线
关于直线 对称的圆的方程为____________
对称的圆的方程为____________