题目内容
( 12分)已知函数f(x)=ax3+bx2的图象经过点M(1,4),曲线在点M处的切线恰好与直线x+9y=0垂直。
(1)求实数a、b的值;(2)若函数f(x)在区间[m,m+1]上单调递增,求m的取值范围.
【答案】
(1)a=1,b=3
(2)m≥0或m≤-3
【解析】 (1)∵f(x)=ax3+bx2的图象经过点M(1,4),
∴a+b=4.①
f′(x)=3ax2+2bx,则f′(1)=3a+2b,
由条件f′(1)·(-)=-1,即3a+2b=9,②
由①②式解得a=1,b=3.
(2)f(x)=x3+3x2,f′(x)=3x2+6x,令f′(x)=3x2+6x≥0得x≥0或x≤-2,
∴f(x)的单调递增区间为(-∞,-2]和[0,+∞)由条件知m≥0或m+1≤-2,
∴m≥0或m≤-3.

练习册系列答案
相关题目
 的定义域为集合A,
的定义域为集合A,  的值域为集合B.
的值域为集合B. ,求
,求 ;
; ,求实数
,求实数 的取值范围。
的取值范围。 的导函数
的导函数 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图象上.
的图象上.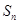 的最大值;
的最大值; ,其中
,其中 ,求
,求 的前
的前 是偶函数.
是偶函数. 有解,求m的取值范围.
有解,求m的取值范围.