题目内容
9.已知函数f(x)=4x2-4ax+a2-2a+2.(1)若函数f(x)在区间[0,2]上的最大值记为g(a),求g(a)的解析式;
(2)若函数f(x)在区间[0,2]上的最小值为3,求实数a的值.
分析 (1)f(x)=$4(x-\frac{1}{2}a)^{2}$+2-2a.对$\frac{1}{2}$a与0,2的大小关系分类讨论,利用二次函数的单调性即可得出.
(2)利用讨论的函数的单调性即可得出.
解答 解:(1)f(x)=4x2-4ax+a2-2a+2=$4(x-\frac{1}{2}a)^{2}$+2-2a.
①当$\frac{1}{2}a≤$0时,函数f(x)在区间[0,2]上单调递增,∴g(a)=f(2)=a2-10a+18;
②当$\frac{1}{2}a≥2$时,函数f(x)在区间[0,2]上单调递减,∴g(a)=f(0)=a2-2a+2;
③当$0<\frac{1}{2}a<2$时,函数f(x)在区间[0,$\frac{1}{2}$a)上单调递减,在区间$(\frac{1}{2}a,2]$上单调递增,∴g(a)=max{f(0),f(2)}.
∴g(a)=$\left\{\begin{array}{l}{{a}^{2}-10a+18,a≤0}\\{{a}^{2}-2a+2,a≥4}\\{max\{f(0),f(2)\},0<a<4}\end{array}\right.$.
(2)由(1)可得:
①当$\frac{1}{2}a≤$0时,函数f(x)在区间[0,2]上单调递增,∴当x=0时,函数f(x)取得最小值,f(0)=a2-2a+2=3,解得a=1-$\sqrt{2}$;
②当$\frac{1}{2}a≥2$时,函数f(x)在区间[0,2]上单调递减,∴当x=2时,函数f(x)取得最小值,f(2)=a2-10a+18=3,解得a=5+$\sqrt{10}$;
③当$0<\frac{1}{2}a<2$时,函数f(x)在区间[0,$\frac{1}{2}$a)上单调递减,在区间$(\frac{1}{2}a,2]$上单调递增,∴当x=$\frac{1}{2}a$时,函数f(x)取得最小值,f($\frac{1}{2}a$)=2-2a=3,解得a=-$\frac{1}{2}$,舍去.
综上可得a=1-$\sqrt{2}$;或5+$\sqrt{10}$.
点评 本题考查了分类讨论、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案| A. | a≤0 | B. | a<1 | C. | a<2 | D. | a<$\frac{1}{3}$ |
| A. | {x|x≥0} | B. | {x|x>0} | C. | {x|x∈R,x≠0} | D. | R |
| A. | (0,2) | B. | (0,1)∪(1,2) | C. | (0,1)和(1,2) | D. | (-∞,0)和(2,+∞) |
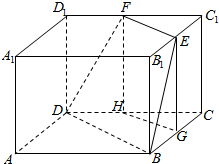 如图.长方体ABCD-A1B1C1D1中,E,F分别是B1C1,C1D1上的点,G,H分别是BC,CD上的点.
如图.长方体ABCD-A1B1C1D1中,E,F分别是B1C1,C1D1上的点,G,H分别是BC,CD上的点.