题目内容
【题目】已知点F1(﹣1,0),F2(1,0),动点M到点F2的距离是 ![]() ,线段MF1的中垂线交线段MF2于点P. (Ⅰ)当点M变化时,求动点P的轨迹G的方程;
,线段MF1的中垂线交线段MF2于点P. (Ⅰ)当点M变化时,求动点P的轨迹G的方程;
(Ⅱ)过点F2且不与x轴重合的直线L与曲线G相交于A,B两点,过点B作x轴的平行线与直线x=2相交于点C,则直线AC是否恒过定点,若是请求出该定点,若不是请说明理由.
【答案】解:(Ⅰ)∵P在线段MF1的中垂线上,∴PM=PF1 , 又P在线段MF2上,∴PM+PF2=MF2=2 ![]() ,
,
∴PF1+PF2=2 ![]() ,而F1F2=2,
,而F1F2=2,
∴动点P的轨迹G是以F1 , F2为焦点的椭圆,
设椭圆方程为 ![]() ,则2a=2
,则2a=2 ![]() ,c=1,∴a=
,c=1,∴a= ![]() ,b=1,
,b=1,
∴动点P的轨迹方程为 ![]() .
.
(Ⅱ)①当l的斜率不存在时,不妨取 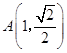 ,
, 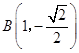 ,
,
∴C(2,﹣ ![]() ),直线AC的方程为
),直线AC的方程为 ![]() x+y﹣
x+y﹣ ![]() =0,
=0,
此时易知AC过点 ![]() .
.
②当l的斜率存在时,设l的方程为:y=k(x﹣1)
联立方程组 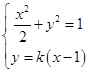 ,消去y得:(1+2k2)x2﹣4k2x+2k2﹣2=0,
,消去y得:(1+2k2)x2﹣4k2x+2k2﹣2=0,
设A(x1 , y1)、B(x2 , y2),则C(2,y2),且x1+x2= ![]() ,
, ![]() ,
,
直线AC方程为 ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= 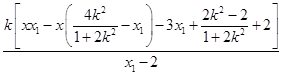 =
= 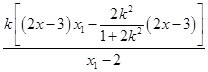 .
.
当 ![]() 时,y=0;
时,y=0;
综上可知,直线AC恒过定点 ![]() .
.
【解析】(I)由中垂线性质可得PM+PF2=MF2=2 ![]() ,故而P点轨迹为F1 , F2为焦点的椭圆,利用定义求出a,b即可得出方程;(II)讨论直线l的斜率,联立方程组,利用根与系数的关系求出直线AC的方程,根据方程判断即可.
,故而P点轨迹为F1 , F2为焦点的椭圆,利用定义求出a,b即可得出方程;(II)讨论直线l的斜率,联立方程组,利用根与系数的关系求出直线AC的方程,根据方程判断即可.

【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如表:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.80 |
该公司从注册的会员中,随机抽取了100位进行统计,得到统计数据如表:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
频数 | 60 | 20 | 10 | 5 | 5 |
假设汽车美容一次,公司成本为150元,根据所给数据,解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(3)设该公司从至少消费两次,求这的顾客消费次数用分层抽样方法抽出8人,再从这8人中抽出2人发放纪念品,求抽出2人中恰有1人消费两次的概率.