题目内容
19.如果一个点是一个指数函数的图象与一个对数函数的图象的公共点,那么称这个点为“好点”,在下面的六个点M(1,1)、N(1,2)、P(1,3)、Q(2,1)、R(2,2)、T(2,3)中,“好点”的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据“好点”的定义,只要判断点在指数函数和对数函数图象上即可.
解答 解:设对数函数为f(x)=logax,指数函数为g(x)=bx,
对于点M,∵f(1)=loga1=0,∴M(1,1)不在对数函数图象上,故M(1,1)不是“好点”.
对于N,∵f(1)=loga1=0,∴N(1,2)不在对数函数图象上,故N(1,2)不是“好点”.
对于P,∵f(1)=loga1=0,∴P(1,3)不在对数函数图象上,故P(1,3)不是“好点”.
对于点Q,∵f(2)=loga2=1,∴a=2,即Q(2,1)在对数函数图象上,
∵g(2)=b2=1,解得b=1,不成立,即Q(2,1)不在指数函数图象上,故Q(2,1)不是“好点”.
对于R∵f(2)=loga2=2,∴a=$\sqrt{2}$,即R(2,2)在对数函数图象上,
∵g(2)=b2=2,解得b=$\sqrt{2}$,即Q(2,2)在指数函数图象上,故Q(2,2)是“好点”.
对于T,f(2)=loga2=3,∴a=$\root{3}{2}$,即T(2,3)在对数函数图象上,
∵g(2)=b2=3,解得b=$\sqrt{3}$,即T(2,3)在指数函数图象上,故T(2,3)是“好点”.
故R,T是“好点”,
故选:B.
点评 本题主要考查与指数函数和对数函数有关的新定义,定义的实质是解指数方程和对数方程.

练习册系列答案
相关题目
4.下列函数中,在区间[0,2]上是增函数的是( )
| A. | y=x2-4x+5 | B. | y=log${\;}_{\frac{1}{2}}$x | C. | y=2-x | D. | y=$\sqrt{x}$ |
11.已知$cos({α+\frac{π}{6}})=\frac{1}{3}$,$α∈[{0,\frac{π}{2}}]$,那么cosα等于( )
| A. | $\frac{2\sqrt{2}-\sqrt{3}}{6}$ | B. | $\frac{2\sqrt{2}+\sqrt{3}}{6}$ | C. | $\frac{2\sqrt{3}-\sqrt{2}}{6}$ | D. | $\frac{2\sqrt{3}+\sqrt{2}}{6}$ |

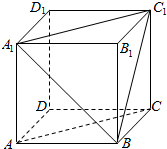 如图,在正方体A1B1C1D1-ABCD中,
如图,在正方体A1B1C1D1-ABCD中,