题目内容
已知函数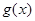 是
是 上的奇函数,且当
上的奇函数,且当 时
时 ,函数
,函数 若
若 >
> ,则实数
,则实数 的取值范围是
的取值范围是
A. | B. |
| C.(1,2) | D. |
D
解析试题分析:∵奇函数g(x)满足当x<0时,g(x)=-ln(1-x),
∴当x>0时,g(-x)=-ln(1+x)=-g(x),
得当x>0时,g(x)=-g(-x)=ln(1+x)
∴f(x)的表达式为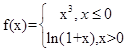 ,
,
∵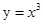 在(-∞,0)上是增函数,y=ln(1+x)在(0,+∞)上是增函数,
在(-∞,0)上是增函数,y=ln(1+x)在(0,+∞)上是增函数,
∴f(x)在其定义域上是增函数,
由此可得: >
> 等价于
等价于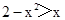 ,解之得-2<x<1,
,解之得-2<x<1,
故选D。
考点:本题主要考查分段函数的概念,函数的奇偶性、单调性,简单不等式的解法。
点评:中档题,涉及抽象函数不等式问题,一般的要通过研究函数的单调性,转化成具体不等式求解。本题定义 人为地增大了难度,易于出错。
人为地增大了难度,易于出错。

练习册系列答案
相关题目
函数 的单调减区间为 ( )
的单调减区间为 ( )
A. | B.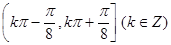 |
C. | D. |
对任意的实数 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
已知函数 ,若
,若 ,则实数a的取值范围是
,则实数a的取值范围是
A. | B. |
C. | D. |
若函数 有两个不同的零点
有两个不同的零点 ,且
,且 ,那么在
,那么在 两个函数值中 ( )
两个函数值中 ( )
| A.只有一个小于1 | B.至少有一个小于1 |
| C.都小于1 | D.可能都大于1 |
函数f(x)=x2-3x+2的零点是( )
A. 或 或 | B. 或 或 |
| C.1或2 | D.-1或-2 |
函数 ,满足
,满足 的
的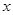 的取值范围( )
的取值范围( )
A. | B. | C. | D. |
下图给出4个幂函数的图象,则图象与函数的大致对应是( )
A.① ② ② ③ ③ ④ ④ |
B.① ② ② ③ ③ ④ ④ |
C.① ② ② ③ ③ ④ ④ |
D.① ② ② ③ ③ ④ ④ |
 是以
是以 为周期的偶函数,当
为周期的偶函数,当 时,
时, .若关于
.若关于 的方程
的方程 (
( )在区间
)在区间 内有四个不同的实根,则
内有四个不同的实根,则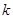 的取值范围是
的取值范围是


