题目内容
【题目】平面几何中，有边长为
的正三角形内任意点到三边距离之和为定值
．类比上述命题，棱长为的正四面体内任一点到四个面的距离之和为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
我们可以根据已知中平面几何中，关于线的性质“正三角形内任意一点到三边距离之和是一个定值”，推断出一个空间几何中一个关于面的性质，利用特殊点，取正四面体外接球的球心即可.
类比在边长为
的正三角形内任一点到三边的距离之和为定值
，
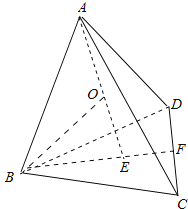
在一个正四面体中，计算一下棱长为的正四面体内任一点到各个面的距离之和，如图：
取正四面体外接球的球心O
由棱长为可以得到
，
，
，
在直角三角形中，根据勾股定理可以得到
，
把数据代入得到
，
∴棱长为的正四面体内任一点到各个面的距离之和
，
故选B．
练习册系列答案
名校课堂系列答案
相关题目
