题目内容
6.数列{an}是等比数列,若a2=1,a5=$\frac{1}{8}$,设Sn=a1a2+a2a3+…+anan+1,若3Sn≤m2+2m对任意n∈N*恒成立,则m的取值范围为( )| A. | -4≤m≤2 | B. | m≤-4或m≥2 | C. | -2≤m≤4 | D. | m≤-2或m≥4 |
分析 由题意可得数列{an}是首项a1=2,公比q=$\frac{1}{2}$的等比数列,求出通项公式,可得数列{anan+1 }是公比为$\frac{1}{4}$的等比数列,利用等比数列的前n项和公式 求出a1a2+a2a3+…+anan+1的最大值,利用3Sn≤m2+2m对任意n∈N*恒成立,即可求出m的取值范围.
解答 解:由数列{an}是等比数列,a2=1,a5=$\frac{1}{8}$,可得公比q=$\frac{1}{2}$,首项a1=2,
∴an=22-n,an+1=21-n,∴anan+1 =23-2n,∴a1a2=2,
故数列{anan+1 }是公比为$\frac{1}{4}$的等比数列,∴a1a2+a2a3+…+anan+1 =$\frac{2(1-\frac{1}{{4}^{n}})}{1-\frac{1}{4}}$<$\frac{8}{3}$,
∵3Sn≤m2+2m对任意n∈N*恒成立,
∴8≤m2+2m,
∴m≤-4或m≥2.
故选:B.
点评 本题考查等比数列的性质,等比数列的通项公式,等比数列的前n项和公式,判断数列{anan+1 }是公比为4的等比数列,是解题的关键.

练习册系列答案
相关题目
16.两直线x+y-1=0,x+y+1=0的距离是( )
| A. | 2 | B. | 1 | C. | 3 | D. | $\sqrt{2}$ |
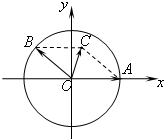 如图,在平面直角坐标系xOy上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).
如图,在平面直角坐标系xOy上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).