题目内容
.如图,在四面体
 中,
中,  平行于截面
平行于截面
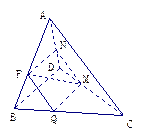
(1)若
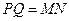 ,证明
,证明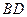 ∥平面
∥平面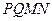 ;
;(2)若
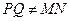 ,猜想三条直线
,猜想三条直线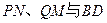 位置关系,并证明之.
位置关系,并证明之.)证明:(1) 因为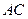 平行截面
平行截面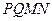 ,
,
则有直线与平面的性质定理得到AC∥PQ,且AC∥MN, 又因为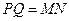 ,
,
所以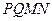 为平行四边形,再有直线与平面的判定定理易得
为平行四边形,再有直线与平面的判定定理易得 ∥平面
∥平面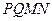 。
。
(2)若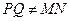 ,则直线PN与直线QM必相交于一点G,又因为
,则直线PN与直线QM必相交于一点G,又因为 ,
,  ,所以
,所以 ,
, .所以
.所以 ,于是三条直线
,于是三条直线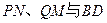 相交于一点。
相交于一点。
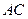 平行截面
平行截面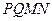 ,
,则有直线与平面的性质定理得到AC∥PQ,且AC∥MN, 又因为
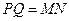 ,
,所以
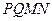 为平行四边形,再有直线与平面的判定定理易得
为平行四边形,再有直线与平面的判定定理易得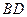 ∥平面
∥平面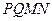 。
。(2)若
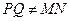 ,则直线PN与直线QM必相交于一点G,又因为
,则直线PN与直线QM必相交于一点G,又因为 ,
,  ,所以
,所以 ,
, .所以
.所以 ,于是三条直线
,于是三条直线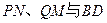 相交于一点。
相交于一点。略

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 中,
中, ,
,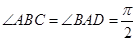 ,
,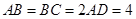 ,
, 、
、 分别是
分别是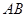 、
、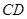 上的动点,且
上的动点,且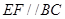 ,设
,设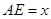 (
(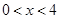 )。沿
)。沿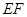 将梯形
将梯形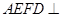 平面
平面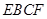 ,如图(2)。
,如图(2)。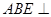 平面
平面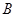 、
、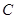 、
、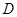 、
、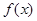 ,求
,求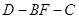 的正弦值.
的正弦值.
 中,
中, ,
, ,
, ,
, 是
是 的中点. 现沿
的中点. 现沿 把平面
把平面 折起,使得
折起,使得 (如图乙所示),
(如图乙所示), 、
、 分别为
分别为 、
、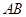 边的中点.
边的中点. 平面
平面 ;
;  平面
平面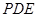 ;
; 上找一点
上找一点 ,使得
,使得 平面
平面
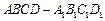 中,设
中,设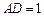 ,
,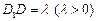 ,
, 上存在点
上存在点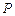 满足
满足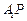
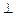 平面
平面 ,求实数
,求实数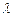 的取值范围
的取值范围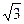 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.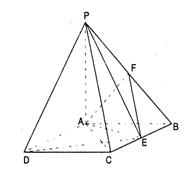
 ,m,n是直线. 给出下列命题:
,m,n是直线. 给出下列命题: 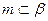 ,则α⊥β
,则α⊥β 是
是 所在平面外上点, 点
所在平面外上点, 点 是点
是点 内的射影.若
内的射影.若 .则点
.则点 是
是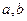 是两条直线,
是两条直线,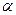 、
、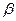 是两个平面,则下列命题中错误的是
是两个平面,则下列命题中错误的是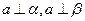 ,则
,则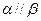
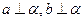 ,则
,则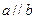
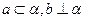 则
则 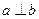
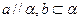 则
则