题目内容
已知点P是双曲线
-
=1(a>0,b>0)右支上一点,F1、F2分别是双曲线的左、右焦点.I为△PF1F2内心,若S△IPF1=S△IPF2+
S△IF1F2,则双曲线的离心率为
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
2
2
.分析:设圆I与△PF1F2的三边F1F2、PF1、PF2分别相切于点E、F、G,连接IE、IF、IG,可得△IF1F2,△IPF1,△IPF2可看作三个高相等且均为圆I半径r的三角形.利用三角形面积公式,代入已知式S△IPF1=S△IPF2+
S△IF1F2,化简可得|PF1|-|PF2|=
|F1F2|,再结合双曲线的定义与离心率的公式,可求出此双曲线的离心率.
| 1 |
| 2 |
| 1 |
| 2 |
解答: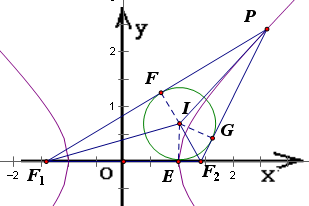 解:如图,设圆I与△PF1F2的三边F1F2、PF1、PF2分别相切于点E、F、G,连接IE、IF、IG,
解:如图,设圆I与△PF1F2的三边F1F2、PF1、PF2分别相切于点E、F、G,连接IE、IF、IG,
则IE⊥F1F2,IF⊥PF1,IG⊥PF2,它们分别是
△IF1F2,△IPF1,△IPF2的高,
∴S△IPF1=
×|PF1|×|IF|=
|PF1|,
S△IPF2=
×|PF2|×|IG|=
|PF2|
S△IF1F2=
×|F1F2|×|IE|=
|F1F2|,其中r是△PF1F2的内切圆的半径.
∵S△IPF1=S△IPF2+
S△IF1F2
∴
|PF1|=
|PF2|+
|F1F2|
两边约去
得:|PF1|=|PF2|+
|F1F2|
∴|PF1|-|PF2|=|F1F2|
根据双曲线定义,得|PF1|-|PF2|=2a,|F1F2|=2c
∴2a=c⇒离心率为e=
=2
故答案为:2.
 解:如图,设圆I与△PF1F2的三边F1F2、PF1、PF2分别相切于点E、F、G,连接IE、IF、IG,
解:如图,设圆I与△PF1F2的三边F1F2、PF1、PF2分别相切于点E、F、G,连接IE、IF、IG,则IE⊥F1F2,IF⊥PF1,IG⊥PF2,它们分别是
△IF1F2,△IPF1,△IPF2的高,
∴S△IPF1=
| 1 |
| 2 |
| r |
| 2 |
S△IPF2=
| 1 |
| 2 |
| r |
| 2 |
S△IF1F2=
| 1 |
| 2 |
| r |
| 2 |
∵S△IPF1=S△IPF2+
| 1 |
| 2 |
∴
| r |
| 2 |
| r |
| 2 |
| r |
| 4 |
两边约去
| r |
| 2 |
| 1 |
| 2 |
∴|PF1|-|PF2|=|F1F2|
根据双曲线定义,得|PF1|-|PF2|=2a,|F1F2|=2c
∴2a=c⇒离心率为e=
| c |
| a |
故答案为:2.
点评:本题将三角形的内切圆放入到双曲线当中,用来求双曲线的离心率,着重考查了双曲线的基本性质、三角形内切圆的性质和面积计算公式等知识点,属于中档题.

练习册系列答案
相关题目
 = .
= .