题目内容
已知点F是双曲线x2-
=1的一个焦点，过点F作直线l交双曲线于两点P、Q，若|PQ|=4，则这样的直线l有且仅有（ ）
| y2 |
| 2 |
分析：当直线l与双曲线左右各有一个交点时，弦长|PQ|最小为实轴长2a=2，若|PQ|=4，则这样的直线l有且仅有两条，当直线l与双曲线的一支有两个交点时，弦长|PQ|最小为通径长
=4，若|PQ|=4，则这样的直线l有且仅有1条，数形结合即可
| 2b2 |
| a |
解答：解：如图：当直线l与双曲线左右各有一个交点时，弦长|PQ|最小为实轴长2a=2，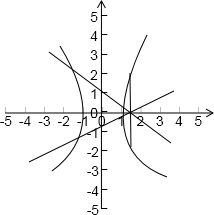
当直线l与双曲线的一支有两个交点时，弦长|PQ|最小为通径长
=4
根据双曲线的对称性可知，若|PQ|=4，则当直线l与双曲线左右各有一个交点时，这样的直线l可有两条，当直线l与双曲线的一支有两个交点时，这样的直线l只有1条，所以若|PQ|=4，则这样的直线l有且仅有3条
故选B
当直线l与双曲线的一支有两个交点时，弦长|PQ|最小为通径长
| 2b2 |
| a |
根据双曲线的对称性可知，若|PQ|=4，则当直线l与双曲线左右各有一个交点时，这样的直线l可有两条，当直线l与双曲线的一支有两个交点时，这样的直线l只有1条，所以若|PQ|=4，则这样的直线l有且仅有3条
故选B
点评：本题考查了双曲线的几何性质，特别是直线与双曲线相交时弦长的几何性质，在平时的学习中注意积累一些结论，对解决此类选择题很有好处
练习册系列答案
相关题目
，求直线l的方程．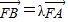
，当λ∈[6，+∞）时，求直线l的斜率k的取值范围．