题目内容
【题目】对于函数
有以下说法：
①
是
的极值点.
②当
时， 
在
上是减函数.
③
的图像与
处的切线必相交于另一点.
④当
时， 
在
上是减函数.
其中说法正确的序号是_______________.
【答案】②③
【解析】由于函数
,则
①由于
在
恒为正或恒为负,故x=0不是f(x)的极值点，故①错误；
②由于a<0时, 
<0在(∞,+∞)上恒成立,则f(x)在(∞,+∞)上是减函数，故②正确；
③由于
,则f′(1)=3a
故f(x)在(1,f(1))处的切线方程：ya=3a(x1)，即：y=3ax2a，
联立y=a
,(a≠0)得到a
=3ax2a,整理得
=0，即
或2， 
的图像与
处的切线
,故③正确；
④当
时， 
在(∞,+∞)上恒成立, 
在
上是增函数函数,故④错误.
故答案为②③.
名校课堂系列答案
【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差 x (℃) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是:先用2、3、4、5月的4组数据求线性回归方程,再用1月和6月的2组数据进行检验.
（1）请根据2、3、4、5月的数据,求出y关于x的线性回归方程
；
（2）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
（参考公式: 
， 
）
参考数据：11×25+13×29+12×26+8×16=
1092，112+132+122+82=498.
【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
【题目】某小型企业甲产品生产的投入成本
（单位：万元）与产品销售收入
（单位：万元）存在较好的线性关系，下表记录了最近5次产品的相关数据.
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
（1）求
关于
的线性回归方程；
（2）根据（1）中的回归方程，判断该企业甲产品投入成本20万元的毛利率更大还是投入成本24万元的毛利率更大（
）？
相关公式：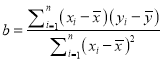 
， 
.
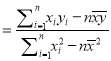【答案】（1）
.（2）投入成本20万元的毛利率更大.
【解析】试题分析：（1）由回归公式，解得线性回归方程为
；（2）当
时， 
，对应的毛利率为
，当
时， 
，对应的毛利率为
，故投入成本20万元的毛利率更大。
试题解析：
（1）
， 
，
， 
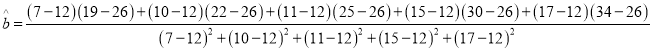
，故
关于
的线性回归方程为
.
（2）当
时， 
，对应的毛利率为
，
当
时， 
，对应的毛利率为
，
故投入成本20万元的毛利率更大.
【题型】解答题
【结束】
21
【题目】已知椭圆
的一个焦点为
.设椭圆
的焦点恰为椭圆
短轴的顶点，且椭圆
过点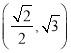
.
（1）求
的方程及离心率；
（2）若直线
与椭圆
交于
两点，求
.