题目内容
【题目】已知矩阵A的逆矩阵A﹣1=
．
（1）求矩阵A；
（2）求矩阵A﹣1的特征值以及属于每个特征值的一个特征向量．
【答案】解：（1）设A=
，则由AA﹣1=E得
=
，
解得a=
，b=﹣
，c=﹣，d=，所以A=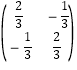
；
（2）矩阵A﹣1的特征多项式为f（λ）=
=（λ﹣2）2﹣1，
令f（λ）=（λ﹣2）2﹣1=0，可求得特征值为λ1=1，λ2=3，
设λ1=1对应的一个特征向量为α=
，
则由λ1α=Mα，得x+y=0
得x=﹣y，可令x=1，则y=﹣1，
所以矩阵M的一个特征值λ1=1对应的一个特征向量为
，
同理可得矩阵M的一个特征值λ2=3对应的一个特征向量为
．
【解析】（1）利用AA﹣1=E，建立方程组，即可求矩阵A；
（2）先根据特征值的定义列出特征多项式，令f（λ）=0解方程可得特征值，再由特征值列出方程组即可解得相应的特征向量．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】甲、乙两同学5次综合测评的成绩如茎叶图所示．
甲 | 乙 | |||||
9 | 8 | 8 | 3 | 3 | 7 | |
2 | 1 | 0 | 9 | ● | 9 |
老师在计算甲、乙两人平均分时，发现乙同学成绩的一个数字无法看清．若从{0，1，2，…，9}随机取一个数字代替，则乙的平均成绩超过甲的平均成绩的概率为（ ）
A.
B.
C.
D.
