题目内容
5．已知椭圆经过点（$\frac{\sqrt{6}}{3}$，$\sqrt{3}$）和点（$\frac{2\sqrt{2}}{3}$，1），求椭圆的标准方程．分析 由题意设椭圆的标准方程为mx2+ny2=1，（其中m、n为正数且m≠n），代点可得m和n的方程组，解方程组可得．
解答 解：由题意设椭圆的标准方程为mx2+ny2=1，（其中m、n为正数且m≠n），
∵椭圆经过点（$\frac{\sqrt{6}}{3}$，$\sqrt{3}$）和点（$\frac{2\sqrt{2}}{3}$，1），
∴$\left\{\begin{array}{l}{\frac{2}{3}m+3n=1}\\{\frac{8}{9}m+n=1}\end{array}\right.$，解方程组可得$\left\{\begin{array}{l}{m=1}\\{n=\frac{1}{9}}\end{array}\right.$，
∴所求椭圆的标准方程为x2+$\frac{{y}^{2}}{9}$=1
点评 本题考查椭圆的标准方程的求解，设方程为mx2+ny2=1可避免分类讨论，是解决问题的关键，属中档题．
练习册系列答案
相关题目
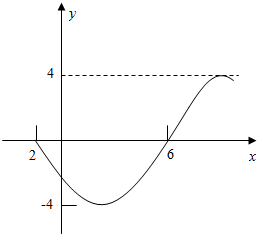函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜π，x∈R）的部分图象如图所示．