题目内容
3.已知函数f(x)=$\frac{\sqrt{1+si{n}^{2}x}+sinx-1}{\sqrt{1+si{n}^{2}x}+sinx+1}$,其中x∈R.(Ⅰ)证明:2π是函数f(x)的周期;
(Ⅱ)①指出并证明函数f(x)的奇偶性;
②写出(不必说明理由)函数y=f(x)图象的一条对称轴;
(Ⅲ)求函数f(x)的值域.
分析 (Ⅰ)由函数的周期性的定义,即可得证;
(Ⅱ)①函数f(x)为奇函数.运用奇函数的定义即可得到;
②x=$\frac{π}{2}$为函数y=f(x)图象的一条对称轴;
(Ⅲ)由f(x)为奇函数,且为周期函数,且对称轴为x=kπ+$\frac{π}{2}$,k∈Z,根据对称轴处取得最值,即可得到值域.
解答 解:(Ⅰ)证明:由-1≤sinx≤1,可得函数f(x)的定义域为R,
f(x+2π)=$\frac{\sqrt{1+si{n}^{2}(x+2π)}+sin(x+2π)-1}{\sqrt{1+si{n}^{2}(x+2π)}+sin(x+2π)+1}$=$\frac{\sqrt{1+si{n}^{2}x}+sinx-1}{\sqrt{1+si{n}^{2}x}+sinx+1}$=f(x),
即有2π是函数f(x)的周期;
(Ⅱ)①函数f(x)为奇函数.
理由如下:f(-x)+f(x)=$\frac{\sqrt{1+si{n}^{2}x}-sinx-1}{\sqrt{1+si{n}^{2}x}-sinx+1}$+$\frac{\sqrt{1+si{n}^{2}x}+sinx-1}{\sqrt{1+si{n}^{2}x}+sinx+1}$
=$\frac{(1+si{n}^{2}x)-(sinx+1)^{2}+(1+si{n}^{2}x)-(sinx-1)^{2}}{(\sqrt{1+si{n}^{2}x}-sinx+1)(\sqrt{1+si{n}^{2}x}+sinx+1)}$
=0,
即有f(-x)=-f(x),f(x)为奇函数.
②x=$\frac{π}{2}$为函数y=f(x)图象的一条对称轴;
(Ⅲ)由f(x)为奇函数,且为周期函数,f(0)=0,且对称轴为x=kπ+$\frac{π}{2}$,k∈Z,
代入x=$\frac{π}{2}$,可得f($\frac{π}{2}$)=$\frac{\sqrt{1+si{n}^{2}\frac{π}{2}}+sin\frac{π}{2}-1}{\sqrt{1+si{n}^{2}\frac{π}{2}}+sin\frac{π}{2}+1}$=$\frac{\sqrt{2}}{\sqrt{2}+2}$=$\sqrt{2}$-1.
代入x=-$\frac{π}{2}$,可得f(-$\frac{π}{2}$)=$\frac{\sqrt{1+si{n}^{2}(-\frac{π}{2})}+sin(-\frac{π}{2})-1}{\sqrt{1+si{n}^{2}(-\frac{π}{2})}+sin(-\frac{π}{2})+1}$=$\frac{\sqrt{2}-2}{\sqrt{2}}$=1-$\sqrt{2}$.
即有函数的值域为[1-$\sqrt{2}$,$\sqrt{2}$-1].
点评 本题考查函数的性质和运用,主要考查三角函数的奇偶性和周期性、对称性的判断和运用,同时考查函数的值域求法,属于中档题.

 发散思维新课堂系列答案
发散思维新课堂系列答案| A. | -sinx | B. | -sinx+x | C. | cosx | D. | cosx+x |
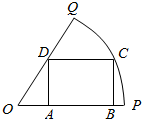 如图所示,扇形OPQ的半径为2,圆心角为$\frac{π}{3}$,C是扇形弧上的动点,四边形ABCD是扇形的内接矩形,则SABCD的最大值是( )
如图所示,扇形OPQ的半径为2,圆心角为$\frac{π}{3}$,C是扇形弧上的动点,四边形ABCD是扇形的内接矩形,则SABCD的最大值是( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{2}{3}$ |