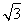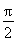题目内容
设平面向量
=(cosx,sinx),
=(
,
),函数f(x)=
•
+1.
①求函数f(x)的值域;
②求函数f(x)的单调增区间.
③当f(α)=
,且
<α<
时,求sin(2α+
)的值.
| a |
| b |
| ||
| 2 |
| 1 |
| 2 |
| a |
| b |
①求函数f(x)的值域;
②求函数f(x)的单调增区间.
③当f(α)=
| 9 |
| 5 |
| π |
| 6 |
| 2π |
| 3 |
| 2π |
| 3 |
依题意f(x)=(cosx,sinx)•(
,
)+1=
cosx+
sinx+1(2分)
=sin(x+
)+1(5分)
①函数f(x)的值域是[0,2];(6分)
②令-
+2kπ≤x+
≤
+2kπ,
解得:-
+2kπ≤x≤
+2kπ,
所以函数f(x)的单调增区间为[-
+2kπ,
+2kπ](k∈Z);(8分)
③由f(α)=sin(α+
)+1=
,得sin(α+
)=
,
因为
<α<
,所以
<α+
<π,
得cos(α+
)=-
,(11分)
则sin(2α+
)=sin2(α+
)
=2sin(α+
)cos(α+
)=-2×
×
=-
(13分).
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=sin(x+
| π |
| 3 |
①函数f(x)的值域是[0,2];(6分)
②令-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得:-
| 5π |
| 6 |
| π |
| 6 |
所以函数f(x)的单调增区间为[-
| 5π |
| 6 |
| π |
| 6 |
③由f(α)=sin(α+
| π |
| 3 |
| 9 |
| 5 |
| π |
| 3 |
| 4 |
| 5 |
因为
| π |
| 6 |
| 2π |
| 3 |
| π |
| 2 |
| π |
| 3 |
得cos(α+
| π |
| 3 |
| 3 |
| 5 |
则sin(2α+
| 2π |
| 3 |
| π |
| 3 |
=2sin(α+
| π |
| 3 |
| π |
| 3 |
| 4 |
| 5 |
| 3 |
| 5 |
| 24 |
| 25 |

练习册系列答案
相关题目