题目内容

设平面向量a=(cosx,sinx),b=(cosx+2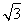,sinx),x∈R.

(1)若x∈(0,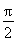),证明:a和b不平行;

(2)若c=(0,1),求函数f(x)=a·(b-2c)的最大值,并求出相应的x值.

 

【答案】

(1)见解析 (2) f(x)max=5,x=2kπ-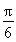(k∈Z)

【解析】

(1)证明:假设a与b平行,

则cosxsinx-sinx(cosx+2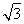)=0,

即sinx=0,与x∈(0,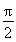)时,sinx>0,矛盾.

故a与b不平行.

(2)解:f(x)=a·b-2a·c

=cos2x+2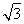cosx+sin2x-2sinx

=1-2sinx+2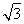cosx

=1-4sin（x-）.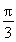

所以f(x)max=5,x=2kπ-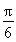(k∈Z).

 

练习册系列答案
相关题目
设平面向量
a
=(cosx，sinx)，
b
=(
3
2
，
1
2
)，函数f(x)=
a
•
b
+1．
①求函数f（x）的值域；
②求函数f（x）的单调增区间．
③当f(α)=
9
5
，且
π
6
＜α＜
2π
3
时，求sin(2α+
2π
3
)的值．
设平面向量
a
=（cosx，sinx），
b
=(cosx+2
3
，sinx)，
c
=(sinα，cosα)，x∈R，
（Ⅰ）若
a
⊥
c
，求cos（2x+2α）的值；
（Ⅱ）若x∈(0，
π
2
)，证明
a
和
b
不可能平行；
（Ⅲ）若α=0，求函数f(x)=
a
•(
b
-2
c
)的最大值，并求出相应的x值．
设平面向量
a
=（cosx，sinx），
b
=（
3
2
，
1
2
），函数f（x）=
a
•
b
+1．
（Ⅰ）求函数f（x）的值域和函数的单调递增区间；
（Ⅱ）当f（a）=
9
5
，且
π
6
＜a＜
2π
3
时，求sin（2a+
2π
3
）的值．
设平面向量
a
=(cosx，sinx)，
b
=(
3
2
，
1
2
)，函数f(x)=
a
•
b
+1．
①求函数f（x）的值域；
②求函数f（x）的单调增区间．
③当f(α)=
9
5
，且
π
6
＜α＜
2π
3
时，求sin(2α+
2π
3
)的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网