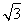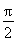题目内容
设平面向量| a |
| b |
| ||
| 2 |
| 1 |
| 2 |
| a |
| b |
①求函数f（x）的值域；
②求函数f（x）的单调增区间．
③当f(α)=
| 9 |
| 5 |
| π |
| 6 |
| 2π |
| 3 |
| 2π |
| 3 |
分析：根据f（x）的特点，利用平面向量的数量积的运算法则化简，然后利用两角和的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数，从而确定出f（x）的解析式，
①根据正弦函数的值域即可求出f（x）的值域；
②根据正弦函数的单调区间为[2kπ-
，2kπ+
]，列出不等式，求出不等式的解集即可得到x的取值范围即为f（x）的递增区间；
③根据f(α)=
，代入f（x）的解析式中，得到sin（α+
）的值，根据α的范围求出α+
的范围，利用同角三角函数间的基本关系求出cos（α+
）的值，把所求的式子利用二倍角的正弦函数公式化简，将sin（α+
）和cos（α+
）的值代入即可求出值．
①根据正弦函数的值域即可求出f（x）的值域；
②根据正弦函数的单调区间为[2kπ-
| π |
| 2 |
| π |
| 2 |
③根据f(α)=
| 9 |
| 5 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
解答：解：依题意f（x）=（cosx，sinx）•(
，
)+1=
cosx+
sinx+1（2分）
=sin(x+
)+1（5分）
①函数f（x）的值域是[0，2]；（6分）
②令-
+2kπ≤x+
≤
+2kπ，
解得：-
+2kπ≤x≤
+2kπ，
所以函数f（x）的单调增区间为[-
+2kπ，
+2kπ](k∈Z)；（8分）
③由f(α)=sin(α+
)+1=
，得sin(α+
)=
，
因为
＜α＜
，所以
＜α+
＜π，
得cos(α+
)=-
，（11分）
则sin(2α+
)=sin2(α+
)
=2sin(α+
)cos(α+
)=-2×
×
=-
（13分）．
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=sin(x+
| π |
| 3 |
①函数f（x）的值域是[0，2]；（6分）
②令-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得：-
| 5π |
| 6 |
| π |
| 6 |
所以函数f（x）的单调增区间为[-
| 5π |
| 6 |
| π |
| 6 |
③由f(α)=sin(α+
| π |
| 3 |
| 9 |
| 5 |
| π |
| 3 |
| 4 |
| 5 |
因为
| π |
| 6 |
| 2π |
| 3 |
| π |
| 2 |
| π |
| 3 |
得cos(α+
| π |
| 3 |
| 3 |
| 5 |
则sin(2α+
| 2π |
| 3 |
| π |
| 3 |
=2sin(α+
| π |
| 3 |
| π |
| 3 |
| 4 |
| 5 |
| 3 |
| 5 |
| 24 |
| 25 |
点评：此题综合考查了正弦函数的定义域及值域，正弦函数的单调性，平面向量的数量积的运算以及三角函数的恒等变换．学生做题时注意角度的范围，灵活运用三角函数公式及平面向量的数量积的运算法则．
练习册系列答案
名校课堂系列答案
相关题目
