题目内容
17.已知实数x,y满足$\left\{{\begin{array}{l}{y≥0}\\{x-y≥0}\\{2x-y-2≥0}\end{array}}\right.$,则x+y-1的取值范围是( )| A. | [-1,3] | B. | [0,4] | C. | [1,+∞) | D. | [0,+∞) |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,通过平移从而求出z的取值范围.
解答 解:作出不等式组对应的平面区域如图:(阴影部分).
设z=x+y-1得y=-x+z+1,即直线的截距最大,z也最大.
平移直线y=-x+z+1,即直线y=-x+z+1经过点A(1,0)时,截距最小,此时z最小,为z=1+0-1=0.
无最大值,
即z≥0,
故z的取值范围是[0,+∞).
故选:D.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案
相关题目
8.已知角α的终边与以坐标原点为圆心,以1为半径的圆交于点P(sin$\frac{2π}{3}$,cos$\frac{2π}{3}$),则角α的最小正值为( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{11π}{6}$ |
9.执行如图的程序框图,则输出的值P=( )
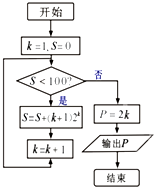

| A. | 12 | B. | 10 | C. | 8 | D. | 6 |
