题目内容
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 为等边三角形,
为等边三角形,![]() ,且
,且![]() ,O,M分别为
,O,M分别为![]() ,
,![]() 的中点.
的中点.
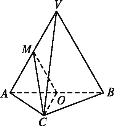
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)设![]() 是线段
是线段![]() 上一点,满足平面
上一点,满足平面![]() 平面
平面![]() ,试说明点的位置
,试说明点的位置![]() ;
;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)详见解析;(Ⅱ)中点;(Ⅲ)![]() .
.
【解析】
试题(Ⅰ)根据线面平行的判定定理,因为O,M分别为![]() ,
,![]() 的中点,所以
的中点,所以![]() ,即可证明
,即可证明![]() 平面
平面![]() ;
;
(Ⅱ)根据面面平行的性质定理,两个平行平面被第三个平面所截,则交线平行,根据已知平面![]() 平面
平面![]() ,与平面
,与平面![]() 交于
交于![]() ,所以
,所以![]() ,则能推出点
,则能推出点![]() 的位置.
的位置.
(Ⅲ)由条件平面![]() 平面
平面![]() ,
,![]() 为等边三角形,所以
为等边三角形,所以![]() ,再根据所给的数据求面积和高,即为体积.
,再根据所给的数据求面积和高,即为体积.
试题解析:(Ⅰ)证明:因为O,M分别为![]() ,
,![]() 的中点,
的中点,
所以![]() .因为
.因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)解:连结ON,MN.因为平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() .
.
因为M为![]() 的中点,所以N为
的中点,所以N为![]() 的中点.
的中点.
(Ⅲ)解:因为![]() ,且
,且![]() ,且O为
,且O为![]() 的中点,
的中点,
所以![]() ,
,![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,可知三棱锥
,可知三棱锥![]() 的体积
的体积![]() .
.
其中,![]() ,
,![]() ,则
,则![]() .
.

练习册系列答案
相关题目
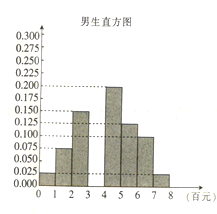
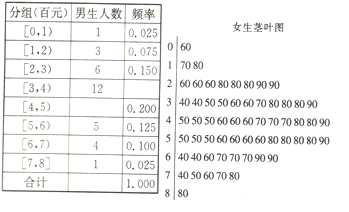
【题目】“双十一”期间,某淘宝店主对其商品的上架时间![]() (小时)和销售量
(小时)和销售量![]() (件)的关系作了统计,得到了如下数据并研究.
(件)的关系作了统计,得到了如下数据并研究.
上架时间 | 2 | 4 | 6 | 8 | 10 | 12 |
销售量 | 64 | 138 | 205 | 285 | 360 | 430 |
(1)求表中销售量![]() 的平均数和中位数;
的平均数和中位数;
(2)① 作出散点图,并判断变量![]() 与
与![]() 是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程
是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程![]() ;
;
②若根据①中线性回归方程得到商品上架12小时的销售量的预测值与检测值不超过3件,则认为得到的线性回归方程是理想的,试问:①中的线性回归方程是否理想.
附:线性回归方程![]() 中,
中, 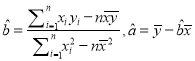 .
.