题目内容
正方体ABCD-A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:
①点E到平面ABC1D1的距离为
;
②直线BC与平面ABC1D1所成的角为45°;
③空间四边形ABCD1在正方体六个面内形成的六个射影平面图形,其中面积最小值是
;
④AE与DC1所成的角的余弦值为
;
⑤二面角A-BD1-C的大小为
.
其中真命题是______.(写出所有真命题的序号)
①点E到平面ABC1D1的距离为
| 1 |
| 2 |
②直线BC与平面ABC1D1所成的角为45°;
③空间四边形ABCD1在正方体六个面内形成的六个射影平面图形,其中面积最小值是
| 1 |
| 2 |
④AE与DC1所成的角的余弦值为
3
| ||
| 10 |
⑤二面角A-BD1-C的大小为
| 5π |
| 6 |
其中真命题是______.(写出所有真命题的序号)
①由于A1B1∥平面ABC1D1,
故B1到平面ABC1D1的距离即点E到平面ABC1D1的距离,
连接B1C交BC1于F,则易得B1F垂直于平面ABC1D1,
而B1F=
,故点E到平面ABC1D1的距离为
,
故①错;
②易得B1C垂直于平面ABC1D1,
故∠CBC1为直线BC与平面ABC1D1所成的角,
且为45°,故②正确;
③易得空间四边形ABCD1在正方体的面ABCD、
面A1B1C1D1内的射影面积为1,在面BB1C1C内、面AA1D1D内的射影面积为
,在面ABB1A1内、面CC1D1D内的射影面积为
,故③正确;
④连接AB1,则∠EAB1为AE与DC1所成的角,由余弦定理得,cos∠EAB1=
=
,故④正确;
⑤在直角三角形BAD1中过A作AH垂直于BD1,连接CH,易知CH垂直于BD1,故∠AHC是二面角A-BD1-C的平面角,由余弦定理得,cos∠AHC=
=-
,故∠AHC=
,故⑤错.
故答案为:②③④
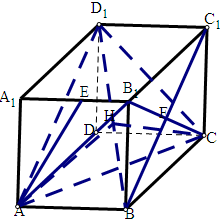
故B1到平面ABC1D1的距离即点E到平面ABC1D1的距离,
连接B1C交BC1于F,则易得B1F垂直于平面ABC1D1,
而B1F=
| ||
| 2 |
| ||
| 2 |
故①错;
②易得B1C垂直于平面ABC1D1,
故∠CBC1为直线BC与平面ABC1D1所成的角,
且为45°,故②正确;
③易得空间四边形ABCD1在正方体的面ABCD、
面A1B1C1D1内的射影面积为1,在面BB1C1C内、面AA1D1D内的射影面积为
| 1 |
| 2 |
| 1 |
| 2 |
④连接AB1,则∠EAB1为AE与DC1所成的角,由余弦定理得,cos∠EAB1=
2+
| ||||||
2×
|
3
| ||
| 10 |
⑤在直角三角形BAD1中过A作AH垂直于BD1,连接CH,易知CH垂直于BD1,故∠AHC是二面角A-BD1-C的平面角,由余弦定理得,cos∠AHC=
| ||||||||
2×
|
| 1 |
| 2 |
| 2π |
| 3 |
故答案为:②③④


练习册系列答案
相关题目