题目内容
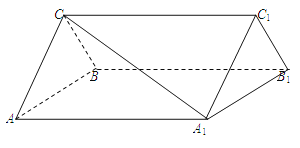
【题目】在直三棱柱![]() 中,
中,![]() 为正三角形,点
为正三角形,点![]() 在棱
在棱![]() 上,且
上,且![]() ,点
,点![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接![]() ,连接
,连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,再连接
,再连接![]() ,证明出
,证明出![]() ,结合条件
,结合条件![]() 可得出
可得出![]() ,然后利用直线与平面平行的判定定理可证明出
,然后利用直线与平面平行的判定定理可证明出![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明出
,证明出![]() 平面
平面![]() ,且
,且![]() ,设等边三角形
,设等边三角形![]() 的边长为
的边长为![]() ,并设
,并设![]() ,以点
,以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,由
,由![]() 得出
得出![]() 的值,并计算出平面
的值,并计算出平面![]() 的法向量,利用空间向量法求出直线
的法向量,利用空间向量法求出直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
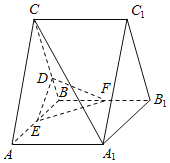
(1)如下图所示,连接![]() ,连接
,连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,再连接
,再连接![]() ,
,
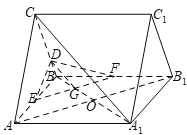
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,则
的中点,则![]() ,
,![]() ,则
,则![]() 为
为![]() 的中点,
的中点,
在直三棱柱![]() 中,
中,![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,
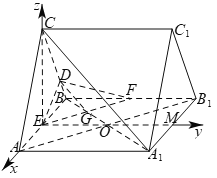
![]() 四边形
四边形![]() 为平行四边形,则
为平行四边形,则![]() ,
,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,所以,四边形
,所以,四边形![]() 是平行四边形,
是平行四边形,
![]() ,在直三棱柱
,在直三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 是等边三角形,且点
是等边三角形,且点![]() 是
是![]() 的中点,
的中点,![]() ,
,
以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
设![]() 的边长为
的边长为![]() ,
,![]() ,则点
,则点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、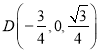 、
、![]() ,
,![]() ,
,![]() ,
,
![]() ,则
,则![]() ,得
,得![]() ,
,
![]() ,
,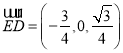 ,
,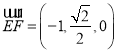 .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由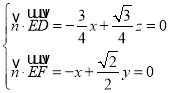 ,得
,得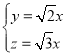 .
.
令![]() ,可得
,可得![]() ,
,![]() ,所以,平面
,所以,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
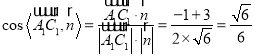 ,
,
因此,直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.

【题目】某工厂的机器上有一种易损元件A,这种元件在使用过程中发生损坏时,需要送维修处维修.工厂规定当日损坏的元件A在次日早上 8:30 之前送到维修处,并要求维修人员当日必须完成所有损坏元件A的维修工作.每个工人独立维修A元件需要时间相同.维修处记录了某月从1日到20日每天维修元件A的个数,具体数据如下表:
日期 | 1 日 | 2 日 | 3 日 | 4 日 | 5 日 | 6 日 | 7 日 | 8 日 | 9 日 | 10 日 |
元件A个数 | 9 | 15 | 12 | 18 | 12 | 18 | 9 | 9 | 24 | 12 |
日期 | 11 日 | 12 日 | 13 日 | 14 日 | 15 日 | 16 日 | 17 日 | 18 日 | 19 日 | 20 日 |
元件A个数 | 12 | 24 | 15 | 15 | 15 | 12 | 15 | 15 | 15 | 24 |
从这20天中随机选取一天,随机变量X表示在维修处该天元件A的维修个数.
(Ⅰ)求X的分布列与数学期望;
(Ⅱ)若a,b![]() ,且b-a=6,求
,且b-a=6,求![]() 最大值;
最大值;
(Ⅲ)目前维修处有两名工人从事维修工作,为使每个维修工人每天维修元件A的个数的数学期望不超过4个,至少需要增加几名维修工人?(只需写出结论)