题目内容
已知函数 ,且
,且 .
. 为
为 的导函数,
的导函数, 的图像如右图所示.若正数
的图像如右图所示.若正数 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( )

A. B.
B. C.
C. D.
D.
【答案】
B
【解析】
试题分析:根据题意,由于函数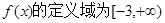 ,且
,且 .,且根据导函数图像可知,x<0递减, 在x>0递增,可知x=0处取得极值,同时那么
.,且根据导函数图像可知,x<0递减, 在x>0递增,可知x=0处取得极值,同时那么 ,则可知-3<2a+b<6,a>0,b>0,因此结合不等式组可知a,b表示的平面区域,然后所求的为点(a,b)与定点(2,-3)的连线的斜率的范围,即可知为
,则可知-3<2a+b<6,a>0,b>0,因此结合不等式组可知a,b表示的平面区域,然后所求的为点(a,b)与定点(2,-3)的连线的斜率的范围,即可知为 ,选B.
,选B.
考点:本试题考查了函数的单调性。
点评:解决该试题的关键是能利用已知的导函数,得到函数的极值点x=0,以及函数单调性,从而确定出使得不等式成立a,b关系式,结合斜率几何意义来求解范围。属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)的导函数为f′(x),且满足关系式f(x)=x2+3xf′(2)+ex,则f'(2)的值等于( )
| A、-0 | ||
B、
| ||
C、-
| ||
D、-
|