题目内容
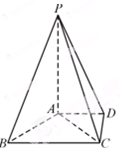
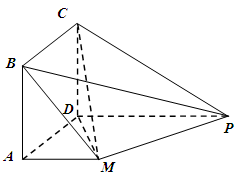
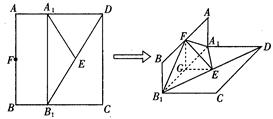
如图,在四棱锥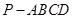 中,
中, 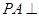 平面
平面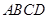 ,
,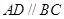 ,
,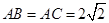 ,
,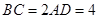 .
.
(Ⅰ)求证: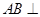 平面
平面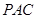 ;
;
(Ⅱ)求棱锥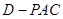 的高.
的高.
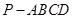 中,
中, 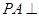 平面
平面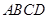 ,
,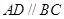 ,
,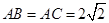 ,
,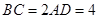 .
. (Ⅰ)求证:
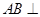 平面
平面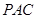 ;
;(Ⅱ)求棱锥
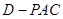 的高.
的高. 
(1)证明见试题解析;(2)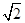 .
.
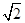 .
.试题分析:(1)要证明线面垂直,需要找出平面中两条相交直线,易知
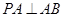 ,根据数量关系,利用勾股定理能够知道
,根据数量关系,利用勾股定理能够知道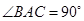 ,即
,即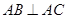 ,从而就能够证出
,从而就能够证出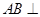 平面
平面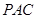 ;(2)解答本题有两种方法.方法一:直接作出高.由
;(2)解答本题有两种方法.方法一:直接作出高.由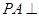 平面
平面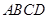 知平面
知平面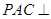 平面
平面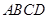 ,在
,在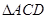 中,过D作
中,过D作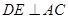 于
于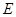 则
则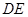 为三棱锥
为三棱锥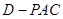 的高,进而求出
的高,进而求出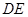 的长.方法二:三棱锥等体积法.根据
的长.方法二:三棱锥等体积法.根据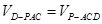 ,则
,则 ,从而求出
,从而求出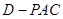 的高
的高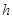 .
.试题解析:(1)证明:
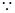
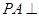 平面
平面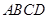
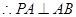
在
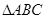 中,
中,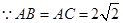 ,
,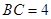
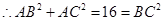
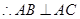
又
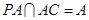
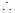
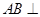 平面
平面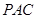
(2)
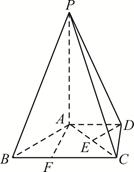
方法一:作出三棱锥的高
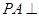 平面
平面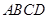 ,
, 平面
平面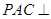 平面
平面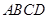
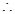 在
在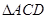 中,过D作
中,过D作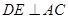 于
于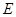 ,则
,则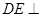 平面
平面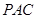
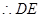 为三棱锥
为三棱锥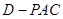 的高
的高 又 在
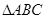 中,过
中,过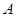 作
作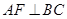 于
于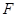 ,则
,则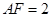
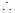 在
在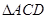 中,
中,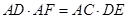
即
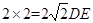 ,
, 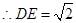
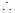 三棱锥
三棱锥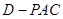 的高为
的高为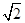
方法二:等体积变换法
在
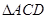 中,过
中,过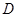 作
作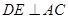 于
于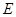 ,
,在
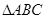 中, 过
中, 过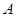 作
作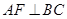 于
于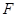 ,则
,则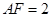
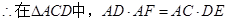
即
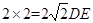 ,
, 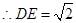
又设三棱锥
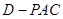 的高为
的高为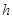 ,
,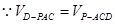 ,
,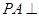 平面
平面
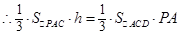 即
即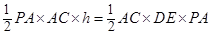
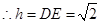
 三棱锥
三棱锥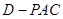 的高为
的高为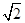

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
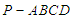 中,底面
中,底面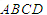 为菱形,
为菱形,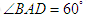 ,
,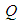 为
为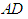 的中点。
的中点。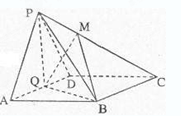
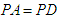 ,求证:平面
,求证:平面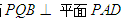 ;
;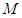 在线段
在线段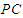 上,
上,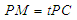 ,试确定
,试确定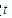 的值,使
的值,使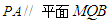 ;
;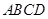 是正方形,
是正方形,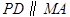 ,
,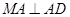 ,
, ,
, 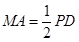 .
.
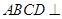 平面
平面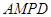 ;
;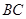 与
与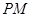 所成的角为
所成的角为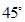 ,求二面角
,求二面角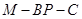 的余弦值.
的余弦值.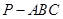 中,
中,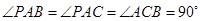 .
.
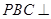 平面
平面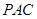 ;
;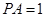 ,
,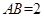 ,当三棱锥
,当三棱锥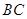 的长.
的长.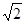 的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为1的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为 .
的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为1的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为 .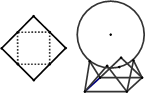
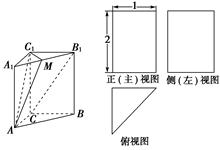
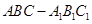 中,
中, 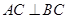 ,
, ,
,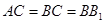 ,点
,点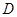 是
是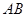 的中点,
的中点,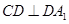 .
.
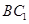 ∥平面
∥平面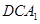 ;
;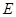 在线段
在线段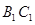 上,
上, ,且使直线
,且使直线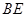 和平面
和平面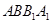 所成的角的正弦值为
所成的角的正弦值为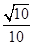 ,求
,求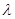 的值.
的值.  折成直角二面角,且
折成直角二面角,且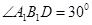 .
.
 的体积.
的体积. 、
、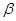 是不同的平面,
是不同的平面,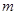 、
、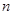 是不同的直线,则下列命题不正确的( )
是不同的直线,则下列命题不正确的( )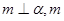 ∥
∥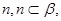 则
则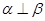
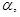
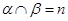 ,则
,则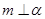 ,则
,则
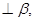 则
则