题目内容
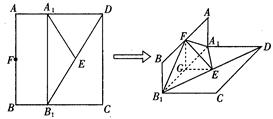
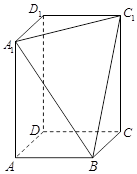
如图,已知长方形ABCD中,AB=2,A1,B1分别是AD,BC边上的点,且AA1=BB1="1," E,F分别为B1D与AB的中点. 把长方形ABCD沿直线 折成直角二面角,且
折成直角二面角,且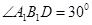 .
.
(1)求证: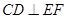
(2)求三棱锥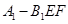 的体积.
的体积.
 折成直角二面角,且
折成直角二面角,且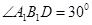 .
.
(1)求证:
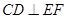
(2)求三棱锥
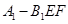 的体积.
的体积.(1)根据题意,由于AA1⊥A1B1,同时FG//AA1,故FG⊥A1B1 ,那么结合A1B1⊥面EFG,可得A1B1⊥EF
得到结论。
(2)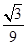
得到结论。
(2)
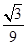
试题分析:解:(I)证明:因为AA1=BB1="1," 且AA1//BB1,所以四边形ABB1A1为矩形,故AA1⊥A1B1,
取A1B1的中点G,边接EG,FG,因为F为AB的中点,所以AF//A1G,且AF=A1G,可得四边形AFGA1是平行四边形,所以FG//AA1,故FG⊥A1B1 ,同理可得EG⊥A1B1,所以A1B1⊥面EFG,可得A1B1⊥EF. 因为CD//A1B1,所以CD⊥EF. (6分)
(II)因为∠A1B1D=30°,所以
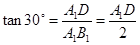 ,
,可得
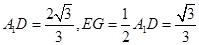 ,因为二面角A-A1B1-D为直二面角,由(I)可知FG⊥面A1B1E, 所以
,因为二面角A-A1B1-D为直二面角,由(I)可知FG⊥面A1B1E, 所以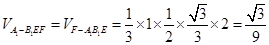 (12分)
(12分)点评:主要是考查了线线垂直以及三棱锥体积的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
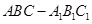 中,
中,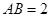 ,
,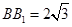 ,
,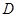 为
为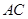 上的动点.
上的动点.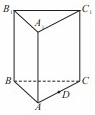
 的体积;
的体积;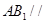 平面
平面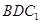 ,请说明理由;
,请说明理由;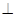 平面
平面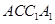 .
.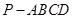 中,
中, 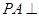 平面
平面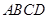 ,
,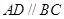 ,
,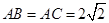 ,
,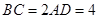 .
. 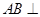 平面
平面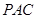 ;
; 的高.
的高. 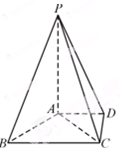
 中,
中, ,
, ,
, 分别是
分别是 上的点,
上的点, ,
, 为
为 的中点.将
的中点.将 沿
沿 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥 ,其中
,其中 .
.
 平面
平面 ;
; 的平面角的余弦值.
的平面角的余弦值.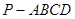 的侧面积为
的侧面积为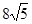 ,若
,若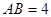 .
.
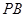 与平面
与平面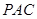 所成角的大小.
所成角的大小.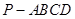 中,
中,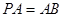 ,点M,N分别在PA,BD上,且
,点M,N分别在PA,BD上,且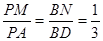 .
.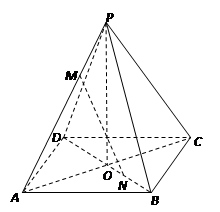
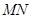 ∥平面PBC;
∥平面PBC;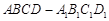 中,
中,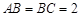 ,过
,过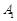 、
、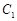 、
、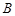 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体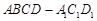 ,且这个几何体的体积为
,且这个几何体的体积为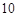 .
.
 的长;
的长; 到平面
到平面 的距离.
的距离.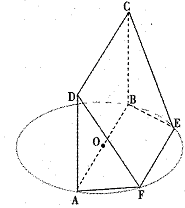
 的底面是正方形,侧棱与底面边长均为2,则其侧视图的面积为_____.
的底面是正方形,侧棱与底面边长均为2,则其侧视图的面积为_____.