题目内容
(本小题共12分)
已知函数f(x)=2x- -aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
-aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
(2)求y=f(x)的极值点(即函数取到极值时点的横坐标).
【答案】
(1)f(x)的单调增区间为(-1,3), 单调减区间为(3,+∞)。
(2)
ⅰ.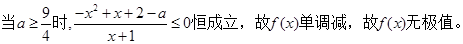 7分
7分
ⅱ.当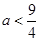 时,
时, 若
若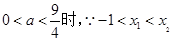 ,由函数的单调性可知f(x)有极小值点
,由函数的单调性可知f(x)有极小值点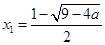 ;有极大值点
;有极大值点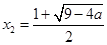 。若
。若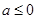 时, f(x)有极大值点
时, f(x)有极大值点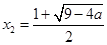 ,无极小值点。
,无极小值点。
【解析】本试题主要是考查了导数在研究函数中的运用。
(1)利用导数的符号与函数单调性的关系求解单调区间。
(2)利用对ad的讨论得到函数的单调性,进而得到最值,求解。
请考生在第22、23三题中任选一题做答,如果多做,则按所做的第一题记分.
(1)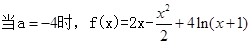
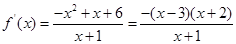
 ……..3分
……..3分
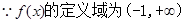 故f(x)的单调增区间为(-1,3), 单调减区间为(3,+∞)………….5分
故f(x)的单调增区间为(-1,3), 单调减区间为(3,+∞)………….5分
(2)∵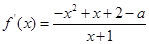
ⅰ.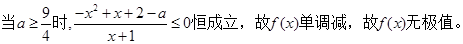 7分
7分
ⅱ.当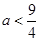 时,对于方程
时,对于方程
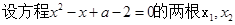 ………………9分
………………9分
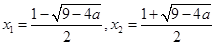
 若
若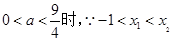 ,由函数的单调性可知f(x)有极小值点
,由函数的单调性可知f(x)有极小值点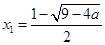 ;有极大值点
;有极大值点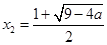 。……………..11分
。……………..11分
若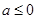 时,
时,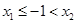 ,由函数的单调性可知f(x)有极大值点
,由函数的单调性可知f(x)有极大值点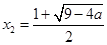 ,无极小值点。………………..12分
,无极小值点。………………..12分

练习册系列答案
相关题目
 ⊥平面
⊥平面 ,
, ∥
∥ 是正三角形,
是正三角形, ,且
,且 是
是 的中点
的中点
 ∥平面
∥平面 ;
; .
. 名,女同学有
名,女同学有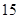 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个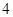 人的课外兴趣小组.
人的课外兴趣小组. 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;


 ,
, ,求证:
,求证: .
. 的值.
的值.