题目内容
在等差数列{an}中,a2=5,a6=21,记数列 的前n项和为Sn,若S2n+1-Sn≤
的前n项和为Sn,若S2n+1-Sn≤ 对n∈N*恒成立,则正整数m的最小值为________.
对n∈N*恒成立,则正整数m的最小值为________.
5
【解析】由题意可知an=4n-3,且(S2n+3-Sn+1)-(S2n+1-Sn)=
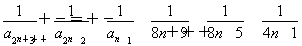 <0,所以{S2n+1-Sn}是递减数列,故(S2n+1-Sn)max=S3-S1=
<0,所以{S2n+1-Sn}是递减数列,故(S2n+1-Sn)max=S3-S1=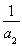 +
+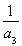 =
=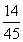 ≤
≤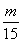 ,解得m≥
,解得m≥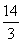 ,故正整数m的最小值为5.
,故正整数m的最小值为5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
在等差数列{an}中,a2=5,a6=21,记数列 的前n项和为Sn,若S2n+1-Sn≤
的前n项和为Sn,若S2n+1-Sn≤ 对n∈N*恒成立,则正整数m的最小值为________.
对n∈N*恒成立,则正整数m的最小值为________.
5
【解析】由题意可知an=4n-3,且(S2n+3-Sn+1)-(S2n+1-Sn)=
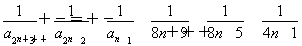 <0,所以{S2n+1-Sn}是递减数列,故(S2n+1-Sn)max=S3-S1=
<0,所以{S2n+1-Sn}是递减数列,故(S2n+1-Sn)max=S3-S1=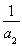 +
+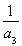 =
=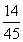 ≤
≤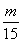 ,解得m≥
,解得m≥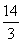 ,故正整数m的最小值为5.
,故正整数m的最小值为5.

 阅读快车系列答案
阅读快车系列答案