题目内容
已知函数 ,则下列说法
,则下列说法①f(x)在[
 )上是减函数;
)上是减函数;②f(x)的最大值是2;
③方程f(x)=0有2个实数根;
④
 在R上恒成立,
在R上恒成立,则下列正确的命题是( )
A.①③④
B.②③④
C.①④
D.①②③
【答案】分析:由函数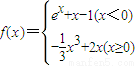 ,分段判断函数在各个区间上的单调性及最值,在求函数单调性时,应用导数求函数的单调区间和最值,从而知道函数的图象的变化情况,故得到答案.
,分段判断函数在各个区间上的单调性及最值,在求函数单调性时,应用导数求函数的单调区间和最值,从而知道函数的图象的变化情况,故得到答案.
解答: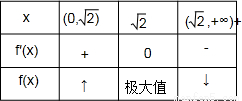 解:当x≥0时,f(x)=
解:当x≥0时,f(x)=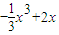 ,令f′(x)=-x2+2=
,令f′(x)=-x2+2=
解得x=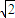 ,∴f′(x)、f(x)随x的变化情况如下表;
,∴f′(x)、f(x)随x的变化情况如下表;
∴函数f(x)在[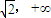 )上是减函数,故①正确;
)上是减函数,故①正确;
当x=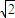 时,f(x)max=
时,f(x)max=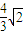 ,故④正确;
,故④正确;
当x<0时,f(x)单调递减,∴f(x)<f(0)=-1
而f(0)=0,当x→+∞时,f(x)→-∞,故方程f(x)=0有2个实数根,故③正确.
故选A.
点评:分段函数求解问题,一般分段求解,体现了分类讨论的数学思想;在探讨函数单调性时,体现了导数的工具性,也培养了应用知识分析、解决问题的能力,是好题,属中档题.
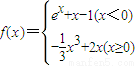 ,分段判断函数在各个区间上的单调性及最值,在求函数单调性时,应用导数求函数的单调区间和最值,从而知道函数的图象的变化情况,故得到答案.
,分段判断函数在各个区间上的单调性及最值,在求函数单调性时,应用导数求函数的单调区间和最值,从而知道函数的图象的变化情况,故得到答案.解答:
 解:当x≥0时,f(x)=
解:当x≥0时,f(x)=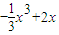 ,令f′(x)=-x2+2=
,令f′(x)=-x2+2=解得x=
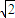 ,∴f′(x)、f(x)随x的变化情况如下表;
,∴f′(x)、f(x)随x的变化情况如下表;∴函数f(x)在[
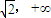 )上是减函数,故①正确;
)上是减函数,故①正确;当x=
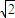 时,f(x)max=
时,f(x)max=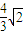 ,故④正确;
,故④正确;当x<0时,f(x)单调递减,∴f(x)<f(0)=-1
而f(0)=0,当x→+∞时,f(x)→-∞,故方程f(x)=0有2个实数根,故③正确.
故选A.
点评:分段函数求解问题,一般分段求解,体现了分类讨论的数学思想;在探讨函数单调性时,体现了导数的工具性,也培养了应用知识分析、解决问题的能力,是好题,属中档题.

练习册系列答案
相关题目
 ,则下列说法正确的是( )
,则下列说法正确的是( ) 有且只有一个零点
B.
有且只有一个零点
B.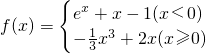 ,则下列说法
,则下列说法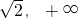 )上是减函数;
)上是减函数;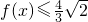 在R上恒成立,
在R上恒成立,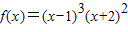 ,则下列说法中正确的是(( )
,则下列说法中正确的是(( ) 处取得极值
处取得极值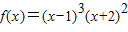 ,则下列说法中正确的是(( )
,则下列说法中正确的是(( ) 处取得极值
处取得极值