题目内容
已知函数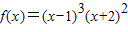 ,则下列说法中正确的是(( )
,则下列说法中正确的是(( )A.在x=l,-2,-
 处取得极值
处取得极值B.既有极大值,也有极小值
C.只有极大值,没有极小值
D.没有极大值,只有极小值
【答案】分析:由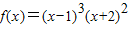 ,知f′(x)=3(x-1)2•(x+2)2+2(x-1)3(x+2)=(x-1)2(x+2)(5x+4),由f′(x)=0,得x1=-2,
,知f′(x)=3(x-1)2•(x+2)2+2(x-1)3(x+2)=(x-1)2(x+2)(5x+4),由f′(x)=0,得x1=-2,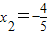 ,x3=1,列表讨论,得函数
,x3=1,列表讨论,得函数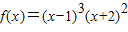 既有极大值,也有极小值.
既有极大值,也有极小值.
解答:解:∵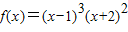 ,
,
∴f′(x)=3(x-1)2•(x+2)2+2(x-1)3(x+2)
=(x-1)2(x+2)[3(x+2)+2(x-1)]
=(x-1)2(x+2)(5x+4),
由f′(x)=0,得x1=-2,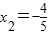 ,x3=1,
,x3=1,
列表讨论,得
∴函数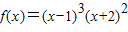 既有极大值,也有极小值.
既有极大值,也有极小值.
故选B.
点评:本题考查函数的极值的求法,解题时要认真审题,仔细解答,注意导数性质的合理运用.
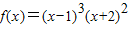 ,知f′(x)=3(x-1)2•(x+2)2+2(x-1)3(x+2)=(x-1)2(x+2)(5x+4),由f′(x)=0,得x1=-2,
,知f′(x)=3(x-1)2•(x+2)2+2(x-1)3(x+2)=(x-1)2(x+2)(5x+4),由f′(x)=0,得x1=-2,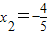 ,x3=1,列表讨论,得函数
,x3=1,列表讨论,得函数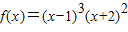 既有极大值,也有极小值.
既有极大值,也有极小值.解答:解:∵
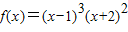 ,
,∴f′(x)=3(x-1)2•(x+2)2+2(x-1)3(x+2)
=(x-1)2(x+2)[3(x+2)+2(x-1)]
=(x-1)2(x+2)(5x+4),
由f′(x)=0,得x1=-2,
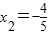 ,x3=1,
,x3=1,列表讨论,得
| x | (-∞,-2) | -2 | (-2,- ) ) | - | (- ,1) ,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + | 0 | + |
| f(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ | ↑ |
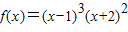 既有极大值,也有极小值.
既有极大值,也有极小值.故选B.
点评:本题考查函数的极值的求法,解题时要认真审题,仔细解答,注意导数性质的合理运用.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 ,则下列说法正确的是( )
,则下列说法正确的是( ) 有且只有一个零点
B.
有且只有一个零点
B.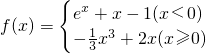 ,则下列说法
,则下列说法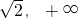 )上是减函数;
)上是减函数;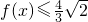 在R上恒成立,
在R上恒成立,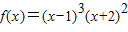 ,则下列说法中正确的是(( )
,则下列说法中正确的是(( ) 处取得极值
处取得极值 ,则下列说法
,则下列说法 )上是减函数;
)上是减函数; 在R上恒成立,
在R上恒成立,